��Ŀ����
��ͼ����֪���ı���ABCD�У�AD��BC��DC��BC����֪AB=5��BC=6��cosB= ����OΪBC���ϵ�һ�����㣬����OD����OΪԲ�ģ�BOΪ�뾶�ġ�O�ֱ�AB�ڵ�P�����߶�OD�ڵ�M��������BC�ڵ�N������MN��
����OΪBC���ϵ�һ�����㣬����OD����OΪԲ�ģ�BOΪ�뾶�ġ�O�ֱ�AB�ڵ�P�����߶�OD�ڵ�M��������BC�ڵ�N������MN����1����BO=ADʱ����BP�ij���
��2����O�˶��Ĺ����У��Ƿ����BP=MN������������ڣ��������BOΪ�ʱBP=MN���������ڣ���˵���ɣ�
��3���ڵ�O�˶��Ĺ����У��Ե�CΪԲ�ģ�CNΪ�뾶����C����ֱ��д������C����ʱ����O���C��λ�ù�ϵ���Լ���Ӧ�ġ�C�뾶CN��ȡֵ��Χ��

���𰸡���������1������A��AE��BC���ڡ�O�У�����O��OH��AB�����ı���ADCE�Ǿ��Σ��������ҵĸ�����AE������AD=CE=BC-BE�����õ�BO=AD��ֵ���ɴ�������֪��PH=BH����BH��OB=cosB�����BH������PB=2BH��
��2���÷�֤����֤��������BP=MN��
��3��������֪������N��BC��ʱ����C���O���У��� ��CN��6=BC������N��BC���ӳ�����ʱ����C���O���У����ڵ�����AB�ϣ�BP�����ֵΪ5������������ҵĸ�����ԲO��ֱ��Ϊ
��CN��6=BC������N��BC���ӳ�����ʱ����C���O���У����ڵ�����AB�ϣ�BP�����ֵΪ5������������ҵĸ�����ԲO��ֱ��Ϊ ����0��CN��
����0��CN�� -6=
-6= ��
��
��� �⣺��1������A��AE��BC
�⣺��1������A��AE��BC
��Rt��ABE����AB=5��cosB= ����BE=3
����BE=3
��CD��BC��AD��BC��BC=6
��AD=EC=BC-BE=3
��BO=AD=3ʱ���ڡ�O�У�����O��OH��AB����BH=HP��
��
��BH=
��BP=
��2��������BP=MN�������
����BP=MN������
��ΪBP��MNΪ��O���ң�����С�BOP=��DOC��
��P��PQ��BC������O��OH��AB��
��CD��BC�����С�PQO�ס�DCO
��BO=x����PO=x��OC=6-x��
�� ����BH=
����BH= ��
��
��BP=2BH=
��BQ=BP×cosB= ��PQ=
��PQ=
��OQ=
�ߡ�PQO�ס�DCO
�� ����
����
��
�� ʱ��BP=
ʱ��BP= =
= ��5�����PӦ�ڱ�AB�ϲ�����
��5�����PӦ�ڱ�AB�ϲ�����
�����BP=MN�������
��3�����һ����O���C�����У���ʱ0��CN��6��
���������O���C�����У���ʱ0��CN�� ��
��
�������������������ҵĸ�����ε����ʡ�����������ֱ�������ε����ʡ����������ε��ж������ʡ�Բ��Բ��λ�ù�ϵ��⣮
��2���÷�֤����֤��������BP=MN��
��3��������֪������N��BC��ʱ����C���O���У���
 ��CN��6=BC������N��BC���ӳ�����ʱ����C���O���У����ڵ�����AB�ϣ�BP�����ֵΪ5������������ҵĸ�����ԲO��ֱ��Ϊ
��CN��6=BC������N��BC���ӳ�����ʱ����C���O���У����ڵ�����AB�ϣ�BP�����ֵΪ5������������ҵĸ�����ԲO��ֱ��Ϊ ����0��CN��
����0��CN�� -6=
-6= ��
�����
 �⣺��1������A��AE��BC
�⣺��1������A��AE��BC��Rt��ABE�У���AB=5��cosB=
 ����BE=3
����BE=3��CD��BC��AD��BC��BC=6
��AD=EC=BC-BE=3
��BO=AD=3ʱ���ڡ�O�У�����O��OH��AB����BH=HP��
��

��BH=

��BP=

��2��������BP=MN�������
����BP=MN������

��ΪBP��MNΪ��O���ң�����С�BOP=��DOC��
��P��PQ��BC������O��OH��AB��
��CD��BC�����С�PQO�ס�DCO
��BO=x����PO=x��OC=6-x��
��
 ����BH=
����BH= ��
����BP=2BH=

��BQ=BP×cosB=
 ��PQ=
��PQ=
��OQ=

�ߡ�PQO�ס�DCO
��
 ����
����
��

��
 ʱ��BP=
ʱ��BP= =
= ��5�����PӦ�ڱ�AB�ϲ�����
��5�����PӦ�ڱ�AB�ϲ����������BP=MN�������
��3�����һ����O���C�����У���ʱ0��CN��6��
���������O���C�����У���ʱ0��CN��
 ��
���������������������ҵĸ�����ε����ʡ�����������ֱ�������ε����ʡ����������ε��ж������ʡ�Բ��Բ��λ�ù�ϵ��⣮

��ϰ��ϵ�д�
 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
�����Ŀ
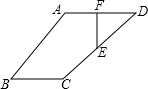 ��ͼ����֪���ı���ABCD�У�E��F�ֱ�ΪAD��DC���е㣬AD��BC��AD��DC=1��
��ͼ����֪���ı���ABCD�У�E��F�ֱ�ΪAD��DC���е㣬AD��BC��AD��DC=1�� ��ͼ����֪ƽ���ı���ABOC�Ķ���A��B��C�ڶ��κ���y=ax2+bx+c��ͼ���ϣ��ֵ�A��B�ֱ���y���x���ϣ���ABO=45�㣮ͼ��ĺ�����Ϊ2������κ�������ʽ��
��ͼ����֪ƽ���ı���ABOC�Ķ���A��B��C�ڶ��κ���y=ax2+bx+c��ͼ���ϣ��ֵ�A��B�ֱ���y���x���ϣ���ABO=45�㣮ͼ��ĺ�����Ϊ2������κ�������ʽ�� ��ͼ����֪���ı���ABCD�У�AD=BC��E��F�ֱ���DC��AB���е㣬ֱ��EF�ֱ���BC��AD���ӳ����ཻ��G��H����֤����AHF=��BGF��
��ͼ����֪���ı���ABCD�У�AD=BC��E��F�ֱ���DC��AB���е㣬ֱ��EF�ֱ���BC��AD���ӳ����ཻ��G��H����֤����AHF=��BGF��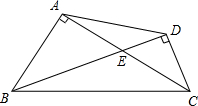 ��2013•������һģ����ͼ����֪���ı���ABCD�У�AC��AB��BD��CD��AC��BD�ཻ�ڵ�E��S��AED=9��S��BEC=25��
��2013•������һģ����ͼ����֪���ı���ABCD�У�AC��AB��BD��CD��AC��BD�ཻ�ڵ�E��S��AED=9��S��BEC=25�� ��ͼ����֪ƽ���ı���ABCD����E��AD���ϵĵ㣬��AE=2ED������BE���ӳ���CD���ӳ����ڵ�F��
��ͼ����֪ƽ���ı���ABCD����E��AD���ϵĵ㣬��AE=2ED������BE���ӳ���CD���ӳ����ڵ�F��