题目内容
如图，已知平行四边形ABCD，点E是AD边上的点，且AE=2ED，连接BE并延长交CD的延长线于点F，| BA |
| a |
| BC |
| b |
| a |
| b |
| BF |
分析：首先利用AB∥CF，得出
=
，进而求出DF，CF与AB的关系，再利用
=
，
=
，得出答案即可．
| AB |
| DF |
| AE |
| ED |
| BA |
| a |
| BC |
| b |
解答：解：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CF，
∴
=
，
∵AE=2ED，
∴DF=
AB，
∴CF=
AB，
∴
=
，
∵
=
，
=
，
∴
=
+
=
+
．
∴AB=CD，AB∥CF，
∴
| AB |
| DF |
| AE |
| ED |
∵AE=2ED，
∴DF=
| 1 |
| 2 |
∴CF=
| 3 |
| 2 |
∴
| CF |
| 3 |
| 2 |
| BA |
∵
| BA |
| a |
| BC |
| b |
∴
| BF |
| BC |
| CF |
| b |
| 3 |
| 2 |
| a |
点评：此题主要考查了平行四边形性质以及平行线的性质和平面向量等知识，根据已知得出
=
+
是解题关键．
| BF |
| BC |
| CF |
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．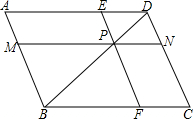
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．