题目内容
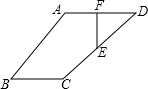 如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:
如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:| 2 |
(1)求AD的长;
(2)△DEF是什么三角形?请你给出正确的判断,并加以说明;
(3)求四边形ABCD的面积.
分析:(1)连接AC,可求得AC的长,根据勾股定理的逆定理,可知∠ACB=90°,由AD∥BC,AD:DC=1:
,可得AD的长;
(2)由三角形中位线的性质,可得EF∥AC,即△DEF是等腰直角三角形;
(3)把四边形ABCD的面积分成两个三角形的面积来求,即S四边形ABCD=S△ABC+S△ACD.
| 2 |
(2)由三角形中位线的性质,可得EF∥AC,即△DEF是等腰直角三角形;
(3)把四边形ABCD的面积分成两个三角形的面积来求,即S四边形ABCD=S△ABC+S△ACD.
解答: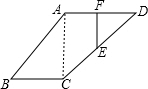 解:(1)如图:连接AC,
解:(1)如图:连接AC,
∵E、F分别为AD、DC的中点,∴AC=2EF,∵EF=4,∴AC=8,
∵AB=10,BC=6,∴△ABC为直角三角形,∴∠ACB=90°,
∵AD∥BC,∴∠CAD=90°,
∵AD:DC=1:
,∴设AD=x,则CD=
x,
即x2+AC2=(
x)2,解得x=8,
∴AD的长为8;
(2)∵EF是△ACD的中位线,∴EF∥AC,∴∠DFE=90°,
∵AD=8,E为AD的中点,
∴DF=EF=4
∴△DEF是等腰直角三角形;
(3)∵S四边形ABCD=S△ABC+S△ACD=AC•BC÷2+AC•AD÷2=8×6÷2+8×8÷2=56.
 解:(1)如图:连接AC,
解:(1)如图:连接AC,∵E、F分别为AD、DC的中点,∴AC=2EF,∵EF=4,∴AC=8,
∵AB=10,BC=6,∴△ABC为直角三角形,∴∠ACB=90°,
∵AD∥BC,∴∠CAD=90°,
∵AD:DC=1:
| 2 |
| 2 |
即x2+AC2=(
| 2 |
∴AD的长为8;
(2)∵EF是△ACD的中位线,∴EF∥AC,∴∠DFE=90°,
∵AD=8,E为AD的中点,
∴DF=EF=4
∴△DEF是等腰直角三角形;
(3)∵S四边形ABCD=S△ABC+S△ACD=AC•BC÷2+AC•AD÷2=8×6÷2+8×8÷2=56.
点评:本题考查了三角形的中位线定理、勾股定理的逆定理以及直角三角形面积的求法.

练习册系列答案
相关题目
 如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.
如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.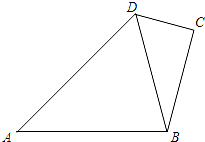 如图,已知在四边形ABCD中,∠C=90°,AB=AD=10,cos∠ABD=
如图,已知在四边形ABCD中,∠C=90°,AB=AD=10,cos∠ABD= 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.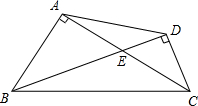 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25. 如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.
如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.