题目内容
 如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为
如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为
- A.2cm
- B.4cm
- C.6cm
- D.8cm
C
分析:利用全等三角形求解.先证明△BDA≌△ACE,从而求得AD=CE=2,BD=AE=4,可求得DE的长.
解答:∵AB=AC,又∠BAC,∠D,∠E为直角,
∴∠C=∠BAD,
∴△BDA≌△ACE,
∴AD=CE,BD=AE,
∵CE=2cm,BD=4cm,
∴DE=6cm.
故选C
点评:本题考查了全等三角形的判定及性质;运用三角形全等的性质对图形进行转换.关键是利用△BDA≌△ACE的性质求得AD=CE=2,BD=AE=4.
分析:利用全等三角形求解.先证明△BDA≌△ACE,从而求得AD=CE=2,BD=AE=4,可求得DE的长.
解答:∵AB=AC,又∠BAC,∠D,∠E为直角,
∴∠C=∠BAD,
∴△BDA≌△ACE,
∴AD=CE,BD=AE,
∵CE=2cm,BD=4cm,
∴DE=6cm.
故选C
点评:本题考查了全等三角形的判定及性质;运用三角形全等的性质对图形进行转换.关键是利用△BDA≌△ACE的性质求得AD=CE=2,BD=AE=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
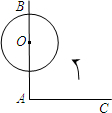 如图所示,∠BAC=90°,O为AB上一点,以O为圆心,
如图所示,∠BAC=90°,O为AB上一点,以O为圆心,| 1 |
| 2 |
| A、30° | B、60° |
| C、60°或120° | D、120° |
 5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )
5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )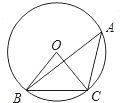 如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB=
如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB= 19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.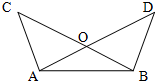 18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,
18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,