题目内容
 19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.(1)△CAB与△DAB全等吗?请说明理由;
(2)试判断OE和AB的位置关系,并给出证明.
分析:(1)由已知条件∠BAC=∠ABD,AC=BD,AB为公共边,用判定定理SAS可判定△CAB与△DAB全等.
(2)由(1)知∠DAB=∠CBA,所以△ABO为等腰三角形,又E是AB的中点,所以OE垂直AB.
(2)由(1)知∠DAB=∠CBA,所以△ABO为等腰三角形,又E是AB的中点,所以OE垂直AB.
解答:解:(1)△CAB与△DAB全等.
理由:∵AC=DB,∠BAC=∠ABD,AB=AB,
∴△CAB与△DAB全等.
(2)垂直.
理由:∵△CAB与△DAB全等,
∴∠BAD=∠ABC,
∴OB=OA,
∴E是AB的中点,
∴AE=BE,
∴△OAE≌△OBE,
∴∠OEA=∠OEB=90°.
即OE与AB垂直.
理由:∵AC=DB,∠BAC=∠ABD,AB=AB,
∴△CAB与△DAB全等.
(2)垂直.
理由:∵△CAB与△DAB全等,
∴∠BAD=∠ABC,
∴OB=OA,
∴E是AB的中点,
∴AE=BE,
∴△OAE≌△OBE,
∴∠OEA=∠OEB=90°.
即OE与AB垂直.
点评:本题考查的三角形全等的判定定理以及等腰三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.一定要牢记.等腰三角形底边的三线合一,也要牢记.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
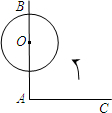 如图所示,∠BAC=90°,O为AB上一点,以O为圆心,
如图所示,∠BAC=90°,O为AB上一点,以O为圆心,| 1 |
| 2 |
| A、30° | B、60° |
| C、60°或120° | D、120° |
 5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )
5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )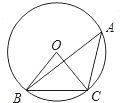 如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB=
如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB=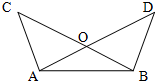 18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,
18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,