题目内容
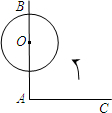 如图所示,∠BAC=90°,O为AB上一点,以O为圆心,
如图所示,∠BAC=90°,O为AB上一点,以O为圆心,| 1 |
| 2 |
| A、30° | B、60° |
| C、60°或120° | D、120° |
分析:将AC绕A点旋转到与圆相切的位置,如图:切点分别为M、N,依题意可得OA=2OM;在Rt△AOM中可求∠MAO的度数,根据切线长定理得∠NAO=∠MAO,由此可求两个旋转角度数.
解答: 解:设AC绕A点旋转过程中,与⊙O分别相切于M、N两点,
解:设AC绕A点旋转过程中,与⊙O分别相切于M、N两点,
由切线的性质可知∠OMA=∠ONA=90°,∠NO=∠MOA,
在Rt△BOM中,AO=2MO,
∴∠MAO=30°,同理可得∠OAN=30°,
∴∠CAM=90°-∠MAO=60°,
∠CAN=90°+∠OAN=120°,
即:旋转角为60°或120°.
故选C.
 解:设AC绕A点旋转过程中,与⊙O分别相切于M、N两点,
解:设AC绕A点旋转过程中,与⊙O分别相切于M、N两点,由切线的性质可知∠OMA=∠ONA=90°,∠NO=∠MOA,
在Rt△BOM中,AO=2MO,
∴∠MAO=30°,同理可得∠OAN=30°,
∴∠CAM=90°-∠MAO=60°,
∠CAN=90°+∠OAN=120°,
即:旋转角为60°或120°.
故选C.
点评:本题考查了旋转,圆的切线的性质,切线长定理等知识.解题时需要注意数形结合思想的应用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )
5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )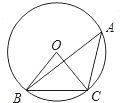 如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB=
如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB= 19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.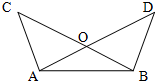 18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,
18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,