题目内容
7. 如图,点A,O,B在同一直线上,∠COD=90°.OE是∠AOD的平分线.
如图,点A,O,B在同一直线上,∠COD=90°.OE是∠AOD的平分线.(1)已知∠BOD=40°,求∠COE的度数;
(2)若∠BOD=50°,则∠COE=25°;
若∠BOD=x°,则∠COE=$\frac{1}{2}$x°(用含x的式子表示)
分析 (1)先根据平角定义求∠AOD的度数,由角平分线可知∠DOE=$\frac{1}{2}$∠AOD,再由∠COD=90°计算出∠COE的度数;
(2)按相同方法将∠BOD=50°代入计算即可得出∠COE=25°;
(3)按相同方法将∠BOD=x°代入计算即可得出∠COE=$\frac{1}{2}$x°.
解答 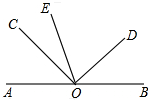 解:(1)∵∠BOD=40°,且∠AOD+∠BOD=180°,
解:(1)∵∠BOD=40°,且∠AOD+∠BOD=180°,
∴∠AOD=180°-40°=140°,
∵OE是∠AOD的平分线,
∴∠DOE=$\frac{1}{2}$∠AOD=70°,
∵∠COD=90°,即∠DOE+∠COE=90°,
∴∠COE=90°-∠DOE=90°-70°=20°;
(2)∵∠BOD=50°,
∴∠AOD=180°-50°=130°,
∵∠DOE=$\frac{1}{2}$∠AOD,
∴∠DOE=65°,
∴∠COE=90°-65°=25°,
(3)∵∠BOD=x°,
∴∠AOD=180°-x°,
∵∠DOE=$\frac{1}{2}$∠AOD,
∴∠DOE=$\frac{1}{2}$(180°-x°)=90°-$\frac{1}{2}$x°,
∴∠COE=90°-(90-$\frac{1}{2}$x)°=$\frac{1}{2}$x°,
故答案为:$\frac{1}{2}$x.
点评 本题考查了平角、直角和角平分线的定义,注意理解角平分线的定义,解题的关键是借助图形找到角与角之间的关系,注意角的和与差.

练习册系列答案
相关题目
18. 如图的图案是由下列四个选项中的哪个图案平移得到的( )
如图的图案是由下列四个选项中的哪个图案平移得到的( )
 如图的图案是由下列四个选项中的哪个图案平移得到的( )
如图的图案是由下列四个选项中的哪个图案平移得到的( )| A. |  | B. |  | C. |  | D. |  |
15.一等腰三角形的周长为8,且各边长都为整数,则腰长为( )
| A. | 4 | B. | 2 | C. | 3 | D. | 2或3 |
12.学习了统计知识后,数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形和扇形统计图.依据图中信息,得出下列结论中正确的是( )


| A. | 接受这次调查的家长人数为180人 | |
| B. | 在扇形统计图中,“不赞同”的家长部分所对应的扇形圆心角大小为135° | |
| C. | 表示“无所谓”的家长人数为60人 | |
| D. | 表示“很赞同”的家长人数为20人 |
19.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.抛物线y=2(x-1)2-5的顶点坐标是( )
| A. | (1,5) | B. | (-1,-5) | C. | (1,-5) | D. | (-1,5) |




 如图,△ACB、△ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD交于F,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
如图,△ACB、△ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD交于F,请你在图中找出一对全等三角形,并写出证明它们全等的过程.