题目内容
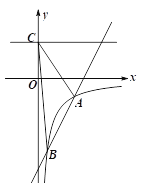
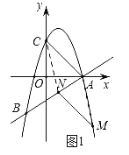
【题目】如图1，在平面直角坐标系中，抛物线
与直线
交于点
和点
，与
轴交于点
.
（1）求出直线和抛物线的函数表达式；
（2）在图1中，平移线段
，恰好可以使得点落在直线上，并且点
落在抛物线上，点、对应的点分别为
、
，求此时点的坐标（点在第四象限）；
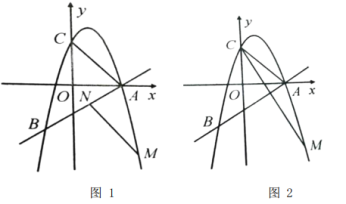
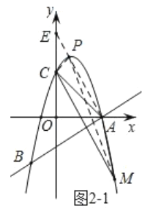
（3）如图2，在（2）的条件下，在抛物线上是否存在点
（不与点重合），使得
面积与
面积相等？若存在，直接写出点的坐标；若不存在，请说明理由.（点在第一象限）
【答案】（1）
；（2）
；（3）存在，P的坐标为（1，4），（2+
，-4-2）或（2-，2-4）．.
【解析】
（1）将点B（-2，-5）代入直线y=x+m即可求出直线解析式，将A（n，0）代入直线解析式y=x-3即可求出点A坐标，将A，B代入抛物线y=-x2+bx+c即可求出抛物线解析式；
（2）先根据直线AB的解析式设出点N坐标，根据平移的性质可知xA-xC=xM-xN，yC-yA=yN-yM，将C，A，N三点坐标代入即可求出含字母的点M的坐标，将M的坐标代入二次函数解析式即可求出M的具体值；
（3）分两种情况讨论，当点P在MC上方的抛物线上时，过点A作CM的平行线交抛物线于点P，交y轴于点E，求出AE的解析式，再求出其与抛物线交点即可，当点P在MC下方的抛物线上时，先找出点E关于点C的对称点O，然后按照相同的方法即可求出点P．
（1）将
代入
，
得
，
∴
，
把
代入，
得
，
∴
，
∴
，
将，代入
，
得
，
解得：
，
，
∴；
（2）∵在中，
当
时，
，
∴
，
∵点
在直线
上，
∴设
，
如图1，由平移的性质知，四边形
是平行四边形，
∴
，
，
∵，，，
∴
，
将代入，
得
，
解得：
（舍去），
，
∴；
（3）①当如图2-1，过点
作
的平行线，交抛物线于点
，交
轴于点
，此时
的面积与
的面积相等，
将，代入
，
得
，
解得：
，
，
∴
，
∵
，
∴设
，
将点代入，
得
，
∴
，
联立与，
得
，
解得：
，
，
∴
.
②当点P在AC下方的抛物线上时，
在yAE=-2x+6中，
当x=0时，y=6，
∴E（0，6），
则点E与原点O关于点C对称，过点O作CM的平行线l，
则yl=-2x，
联立y=-x2+2x+3与yl=-2x，
得-x2+2x+3=-2x，
解得x1=2+，x2=2-，
∴P（2+，-4-2）或（2-，2-4），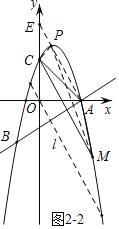
综上所述，P的坐标为（1，4），（2+，-4-2）或（2-，2-4）．
