Question

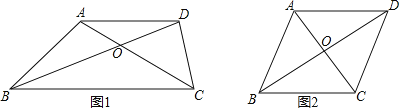
【题目】四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（ ）

A.OA =OB =OC=OD，AC⊥BDB.AB∥CD，AC=BD

C.AD∥BC，∠A=∠CD.OA=OC，OB=OD，AB=AC

Answer 1

【答案】A

【解析】

根据正方形的判定方法逐项判断即可.

解：如图，A、∵OA＝OB＝OC＝OD，∴四边形ABCD是平行四边形，AC＝BD，

∵AC⊥BD，∴四边形ABCD是正方形，故本选项正确；

B、根据AB∥CD和AC＝BD不能推出四边形ABCD是正方形，故本选项错误；

C、∵AD∥BC，∴∠DAB+∠ABC＝180°，∠ADC+∠DCB＝180°，

∵∠DAB＝∠DCB，∴∠ABC＝∠ADC，

∴只能推出四边形ABCD是平行四边形，故本选项错误；

D、∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，

∵AB＝BC，∴只能推出四边形ABCD是菱形，故本选项错误.

故选：A．