题目内容
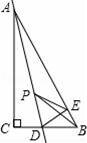
如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .

1+
 .
.
【考点】轴对称-最短路线问题;含30度角的直角三角形;翻折变换(折叠问题).
【专题】几何动点问题.
【分析】连接CE,交AD于M,根据折叠和等腰三角形性质得出当P和D重合时,PE+BP的值最小,即可此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,先求出BC和BE长,代入求出即可.
【解答】

解:连接CE,交AD于M,
∵沿AD折叠C和E重合,
∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,
∴AD垂直平分CE,即C和E关于AD对称,CD=DE=1,
∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,
∵∠DEA=90°,
∴∠DEB=90°,
∵∠B=60°,DE=1,
∴BE=
 ,BD=
,BD=


 ,
,
即BC=1+


 ,
,
∴△PEB的周长的最小值是BC+BE=1+


 +
+


 =1+
=1+
 ,
,
故答案为:1+
 .
.
【点评】本题考查了折叠性质,等腰三角形性质,轴对称﹣最短路线问题,勾股定理,含30度角的直角三角形性质的应用,关键是求出P点的位置,题目比较好,难度适中.

练习册系列答案
相关题目
 -1.33)
-1.33)  经过平移得到抛物线y=
经过平移得到抛物线y= ,其对称轴与两段抛物线所围成的阴影部分的面积为( )
,其对称轴与两段抛物线所围成的阴影部分的面积为( )

 的解是 .
的解是 .



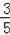
 ,反比例函数y=
,反比例函数y=


 <0 D、|a|>|b|
<0 D、|a|>|b|