Question

如图，在平面直角坐标系中，抛物线y=经过平移得到抛物线y=，其对称轴与两段抛物线所围成的阴影部分的面积为（　　）

A．2       B．4       C．8       D．16

　

Answer 1

B【考点】二次函数图象与几何变换．

【专题】压轴题．

【分析】根据抛物线解析式计算出y=的顶点坐标，过点C作CA⊥y轴于点A，根据抛物线的对称性可知阴影部分的面积等于矩形ACBO的面积，然后求解即可．

【解答】解：过点C作CA⊥y，

∵抛物线y==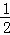（x²﹣4x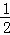）=（x²﹣4x+4）﹣2=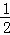（x﹣2）²﹣2，

∴顶点坐标为C（2，﹣2），

对称轴与两段抛物线所围成的阴影部分的面积为：2×2=4，

故选：B．

【点评】本题考查了二次函数的问题，根据二次函数的性质求出平移后的抛物线的对称轴的解析式，并对阴影部分的面积进行转换是解题的关键．