题目内容
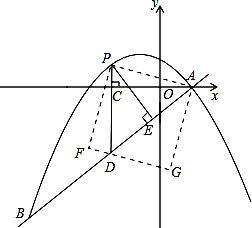
【题目】如图，△ACE是以ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称．若E点的坐标是（7，﹣3
），则D点的坐标为（ ）
A. （3，0）
B. （4，0）
C. （5，0）
D. （6，0）
【答案】C
【解析】
作CE与x轴相交于F点，根据关于数轴对称点的坐标特点可得C（7，3
），即CE=6，因为△ACE是等边三角形，利用勾股定理可求得AF的长，进而得到OA的长，再利用平行线的性质即可得到OD的长.
解：
作CE与x轴相交于F点，
∵C与点E关于x轴对称，E（7，﹣3 ），
∴C（7，3），F（7，0），即CF=3，CE=6，OF=7，
∵△ACE是等边三角形，
∴AC= CE=6，
在Rt△ACF中，AF=
=9，
∴OA=AF﹣OF=9﹣7=2，
又∵四边形ABCD为平行四边形，
∴OD=AD﹣OA=BC﹣OA=5，
则D（5，0）.
故选C.
练习册系列答案
相关题目
