题目内容
【题目】如图,在平面直角坐标系中,直线 ![]() 与抛物线
与抛物线 ![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.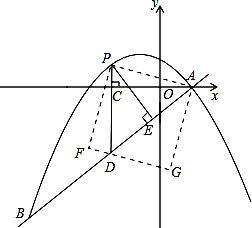
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为 ![]() ,点P的横坐标为
,点P的横坐标为 ![]() ,求
,求 ![]() 关于
关于 ![]() 的函数关系式,并求出
的函数关系式,并求出 ![]() 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在 ![]() 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
【答案】
(1)解:对于 ![]() ,当y=0,x=2.当x=-8时,y=-
,当y=0,x=2.当x=-8时,y=- ![]() .
.
∴A点坐标为(2,0),B点坐标为(-8,- ![]() ).
).
由抛物线 ![]() 经过A、B两点,得
经过A、B两点,得 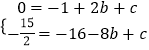 ,解得
,解得 ![]() ,
, ![]() .
.
∴ ![]() ;
;
(2)解:①设直线 ![]() 与y轴交于点M,
与y轴交于点M,
当x=0时,y= ![]() .∴OM=
.∴OM= ![]() .
.
∵点A的坐标为(2,0),∴OA=2.
∴AM= ![]() .
.
∴OM∶OA∶AM=3∶4∶5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,
∴△AOM∽△PED.
∴DE∶PE∶PD=3∶4∶5.
∵点P是直线AB上方的抛物线上一动点,
∵PD⊥x轴,
∴PD两点横坐标相同,
∴PD=yP-yD= ![]() =
= ![]() ,
,
∴ ![]() .
.
∴x=-3时,l最大=15;

②当点G落在y轴上时,如图2,
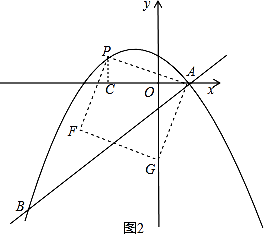
由△ACP≌△GOA得PC=AO=2,
即 ![]() ,解得x=
,解得x= ![]() ,
,
所以P1( ![]() ,2),P2(
,2),P2( ![]() ,2),
,2),
如图3,过点P作PN⊥y轴于点N,过点P作PS⊥x轴于点S,
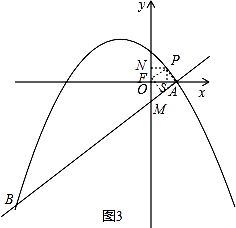
由△PNF≌△PSA,
PN=PS,可得P点横纵坐标相等,
故得当点F落在y轴上时, ![]() ,解得
,解得 ![]() ,
,
可得P3( ![]() ,
, ![]() ),
),
P4( ![]() ,
, ![]() ),(舍去).
),(舍去).
综上所述:满足题意的点P有三个,分别是P1( ![]() ,2),P2(
,2),P2( ![]() ,2),P3(
,2),P3( ![]() ,
, ![]() ).
).
【解析】(1)利用一次函数的解析式当y=0时求出点A的坐标,再将x=-8代入函数解析式求出B的坐标,再利用待定系数法求二次函数解析式解答。
(2)①设z直线AB与y轴交于点M,根据勾股定理求出AM长,及三边之比,再证明△AOM∽△PED.得出DE∶PE∶PD=3∶4∶5,由点P是直线AB上方的抛物线上一动点,PD⊥x轴,得出P、D两点横坐标相同,即可求出PD的长,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答。
②当点G在y轴上时,根据正方形的性质,先证△ACP≌△GOA,得PC=AO=2,根据二次函数的解析式建立方程求解,即可求出点P的坐标;
当点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质,先证△PNF≌△PSA,得出PN=PS,可得P点横纵坐标相等,建立方程求解,即可求出点P的坐标。
【考点精析】利用二次函数的最值和正方形的性质对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案