Question

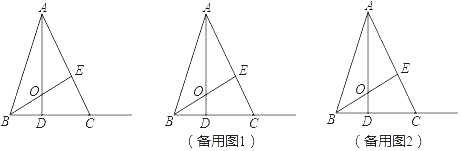
【题目】如图1， ⊙O是等边三角形 的外接圆， 是⊙O上的一个点．

（1）则 =；
（2）试证明： ；
（3）如图2，过点 作⊙O的切线交射线 于点 ．
①试证明： ；
②若 ，求 的长．

Answer 1

【答案】
（1）60°
（2）证明：如图1，在PC上取一点E，使得PE=PA，连结AE，∴△PAE是等边三角形，∴∠PAB=∠EAC，AP=AE，又∵AB=AC，∴△AEC≌△APB，∴PB=EC，∴PA+PB=PE+CE=PC；

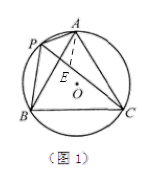
（3）解：①如图2，作⊙O的直径AF，连结PF，则∠PAF+∠F=90°，又∵AD是⊙O的切线，∴∠DAP+∠PAF =90°，∴∠DAP=∠F，∵∠DBA=∠F，∴∠DAP=∠DBA；

②由①可得△DAP∽△DBA，得 ，即 ，∴BD=4，∴PB=3，由①易得△DAP∽△ACP，∴ 即 ，又∵PA+PB=PC，整理得： ，解得PA= ．

【解析】（1）根据等边三角形的性质及同弧所对的圆周角相等，即可得出∠ A P C的度数。
（2）要证PA+PB =PC ，采用截长补短法添加辅助线，在PC上取一点E，使得PE=PA，连结AE，先证明△AEC≌△APB，得出PB=EC，即可证得结论。
（3）①如图2所示，作⊙O的直径AF，连结PF，根据直径所对的圆周角是直角得出∠PAF+∠F=90°，再根据切线的性质得出∠DAP+∠PAF =90°，即可得到∠DAP=∠F，然后根据同弧所对的圆周角相等，即可证得结论。②由①可得△DAP∽△DBA，得出对应边成比例，求出BD的长，再证明△DAP∽△ACP，证得 PA 2 = PC·P D ，又由PA+PB=PC，即可求出PA的长。
【考点精析】利用等边三角形的性质和圆周角定理对题目进行判断即可得到答案，需要熟知等边三角形的三个角都相等并且每个角都是60°；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．