题目内容
12.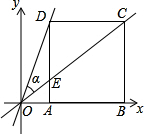 边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.
边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.(1)求点C的坐标;
(2)过O,D两点作直线,记该直线与直线OC的夹角为α,试求tanα的值.
分析 (1)由正方形ABCD的边长为2,得到AB=CD=2,由点A的横坐标为1,得到OA=1,于是得到结论;
(2)过D作DH⊥OC于H,根据相似三角形的性质得到$\frac{AE}{BC}=\frac{OA}{OB}$,求出AE=$\frac{2}{3}$,得到DE=$\frac{4}{3}$,根据勾股定理得到CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\frac{2\sqrt{13}}{3}$,根据三角形的面积得到DH=$\frac{CD•DE}{CE}$=$\frac{4\sqrt{13}}{13}$,根据勾股定理得到OD=$\sqrt{A{D}^{2}+A{O}^{2}}$=$\sqrt{5}$,OH=$\sqrt{O{D}^{2}-D{H}^{2}}$=$\frac{7\sqrt{13}}{13}$,根据三角函数的定义即可得到结论.
解答  解:(1)∵正方形ABCD的边长为2,
解:(1)∵正方形ABCD的边长为2,
∴AB=CD=2,
∵点A的横坐标为1,
∴OA=1,
∴OB=3,
∴C(3,2);
(2)过D作DH⊥OC于H,
∵AD∥BC,
∴△OAE∽△OBC,
∴$\frac{AE}{BC}=\frac{OA}{OB}$,即$\frac{AE}{2}=\frac{1}{3}$,
∴AE=$\frac{2}{3}$,
∴DE=$\frac{4}{3}$,
∴CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\frac{2\sqrt{13}}{3}$,
∴DH=$\frac{CD•DE}{CE}$=$\frac{4\sqrt{13}}{13}$,
在Rt△ADO中,OD=$\sqrt{A{D}^{2}+A{O}^{2}}$=$\sqrt{5}$,
∴OH=$\sqrt{O{D}^{2}-D{H}^{2}}$=$\frac{7\sqrt{13}}{13}$,
∴tanα=$\frac{DH}{OH}=\frac{\frac{4\sqrt{13}}{13}}{\frac{7\sqrt{13}}{13}}$=$\frac{4}{7}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,坐标与图形的性质,勾股定理,三角函数的定义,正确的作出辅助线是解题的关键.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案| A. | x$≤-\frac{1}{2}$ | B. | x$≥-\frac{1}{2}$ | C. | x$<-\frac{1}{2}$ | D. | x$>-\frac{1}{2}$ |
| 月用水量(m3) | 4 | 6 | 7 | 12 | 14 | 15 |
| 户数 | 2 | 4 | 6 | 2 | 2 | 4 |
(2)计算这20户家庭的平均月用水量;
(3)根据上述数据,估计该小区300户家庭的月总用水量.
| 年龄 | 13 | 14 | 15 | 16 |
| 频数 | 1 | 4 | 5 | 2 |
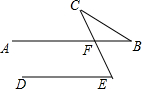 如图,AB∥DE,∠E=60°,则∠B+∠C=60°.
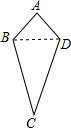
如图,AB∥DE,∠E=60°,则∠B+∠C=60°. 研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;