题目内容
解方程
(1)2x2=3(x+1)
(2)9(x-2)2-121=0
(3)3(x-3)2+x(x-3)=0
(4)x2+4x+2=0(配方法)
(1)2x2=3(x+1)
(2)9(x-2)2-121=0
(3)3(x-3)2+x(x-3)=0
(4)x2+4x+2=0(配方法)
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)整理后求出b2-4ac的值,再代入公式求出即可;
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答:解:(1)2x2=3(x+1),
2x2-3x-3=0,
b2-4ac=(-3)2-4×2×(-3)=33,
x=
,
x1=
,x2=
;
(2)9(x-2)2-121=0,
[3(x-2)+11][3(x-2)-11]=0,
3(x-2)+11=0,3(x-2)-11=0,
x1=-
,x2=
;
(3)3(x-3)2+x(x-3)=0,
(x-3)(3x-9+x)=0,
x-3=0,3x-9+x=0,
x1=3,x2=
;
(4)x2+4x+2=0,
x2+4x=-2,
配方得:x2+4x+4=-2+4,
(x+2)2=2,
开方得:x+2=±
,
x1=-2+
,x2=-2-
.
2x2-3x-3=0,
b2-4ac=(-3)2-4×2×(-3)=33,
x=
3±
| ||
| 2×2 |
x1=
3+
| ||
| 4 |
3-
| ||
| 4 |
(2)9(x-2)2-121=0,
[3(x-2)+11][3(x-2)-11]=0,
3(x-2)+11=0,3(x-2)-11=0,
x1=-
| 2 |
| 3 |
| 17 |
| 3 |
(3)3(x-3)2+x(x-3)=0,
(x-3)(3x-9+x)=0,
x-3=0,3x-9+x=0,
x1=3,x2=
| 9 |
| 4 |
(4)x2+4x+2=0,
x2+4x=-2,
配方得:x2+4x+4=-2+4,
(x+2)2=2,
开方得:x+2=±
| 2 |
x1=-2+
| 2 |
| 2 |
点评:本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
你喜欢吃拉面吗?如图,拉面馆的师傅把一根很粗的面条的两头捏合在一起,拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,若要拉出64根细面条,则需要这样捏合的次数为( )


| A、5 | B、6 | C、7 | D、8 |
方程(x-3)2+2x=6的解是( )
| A、x1=x2=3 |
| B、x1=-3,x2=5 |
| C、x1=3,x2=1 |
| D、x1=3,x2=-1 |
 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.
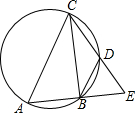 如图,已知△ABC内接于⊙O,D是
如图,已知△ABC内接于⊙O,D是