Question

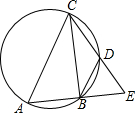如图，已知△ABC内接于⊙O，D是

BC

的一点，连接CD并延长CD，与AB延长线相交于E，BD=BE．
（1）求证：△ACE是等腰三角形；
（2）若AC是⊙O的直径，∠CAB=70°，求

CD

的度数．

Answer 1

考点：圆周角定理,等腰三角形的判定与性质

专题：

分析：（1）由BD=BE与圆的内接四边形的性质，可证得∠A=∠E，即可得：△ACE是等腰三角形；
（2）首先连接OD，易求得∠ACE=40°，继而求得∠COD的度数，即可求得

CD

的度数．

解答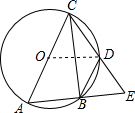：（1）证明：∵BD=BE，
∴∠BDE=∠E，
∵∠BDE+∠BDC=180°，∠BDC+∠A=180°，
∴∠BDE=∠A，
∴∠A=∠E，
∴AC=CE，
即△ACE是等腰三角形；

（2）∵连接OD，
∵∠CAB=70°，AC=CE，
∴∠E=∠A=70°，
∴∠ACE=40°，
∵OC=OD，
∴∠ODC=∠ACE=40°，
∴∠COD=100°，
即

CD

的度数为100°．

点评：此题考查了圆周角定理、等腰三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．