题目内容
20.定义新运算:对于任意有理数a、b,都有a⊕b=a(a-b)+1,等式的右边是通常的有理数运算,例如2⊕5=2(2-5)+1=2×(-3)+1.(1)求(-2)⊕3.
(2)若3⊕x=-5,求x的值.
分析 (1)根据新运算得出原式=-2×(-2-3)+1,求出即可;
(2)根据新运算得出3(3-x)+1=-5,求出方程的解即可.
解答 解:(1)(-2)⊕3=-2×(-2-3)+1=10+1=11;
(2)3⊕x=3(3-x)+1=-5,
9-3x+1=-5,
-3x=-15,
x=5.
点评 本题考查了求代数式的值和有理数的混合运算,能读懂题意是解此题的关键.

练习册系列答案
相关题目
11.在平面直角坐标系中,有A(2,-1)、B(-1,-2)、C(2,1)、D(-2,1)四点.其中,关于原点对称的两点为( )
| A. | 点A和点B | B. | 点B和点C | C. | 点C和点D | D. | 点D和点A |
8.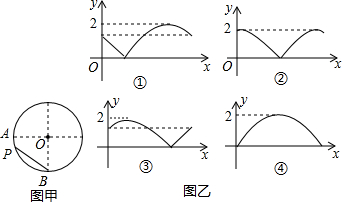 如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )
如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )
 如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )
如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )| A. | ① | B. | ④ | C. | ①或③ | D. | ②或④ |
12.使二次根式$\sqrt{x-7}$有意义的x的取值范围是( )
| A. | 1<x<7 | B. | 0<x≤7 | C. | x≤7 | D. | x≥7 |
5.下列说法中,正确的是( )
| A. | 不可能事件发生的概率为0 | |
| B. | 随机事件发生的概率为0 | |
| C. | 概率很小的事件不可能发生 | |
| D. | 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 |

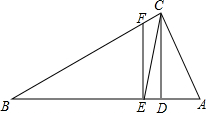 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.