题目内容
7.下列二次根式中,最简二次根式是( )| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{11}$ |
分析 利用最简二次根式定义判断即可.
解答 解:A、原式=2,不符合题意;
B、原式=2$\sqrt{2}$,不符合题意;
C、原式=$\frac{\sqrt{2}}{2}$,不符合题意;
D、原式为最简二次根式,符合题意,
故选D
点评 此题考查了最简二次根式,熟练掌握最简二次根式定义是解本题的关键.

练习册系列答案
相关题目
18.下列命题的逆命题是真命题的是( )
| A. | 对顶角相等 | B. | 全等三角形的面积相等 | ||
| C. | 两直线平行,内错角相等 | D. | 等边三角形是等腰三角形 |
15.在下列调查中,适宜采用全面调查的是( )
| A. | 检测一批灯泡的使用寿命 | |
| B. | 调查昆明《都市条形码》栏目的收视率 | |
| C. | 了解我省中学生视力情况 | |
| D. | 了解九(1)班学生校服的尺码情况 |
12.下列说法正确的是( )
| A. | 0.1$\stackrel{•}{3}$是无理数 | |
| B. | $\frac{4}{11}$是无限小数,是无理数 | |
| C. | $\frac{π}{3}$是分数 | |
| D. | 0.13579…(小数部分由连续的奇数组成)是无理数 |
19.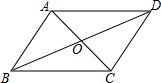 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
16.如果一个角的余角是60°,那么这个角的度数是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
17.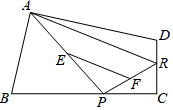 如图所示,已知P、R分别是四边形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么EF的长( )
如图所示,已知P、R分别是四边形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么EF的长( )
 如图所示,已知P、R分别是四边形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么EF的长( )
如图所示,已知P、R分别是四边形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么EF的长( )| A. | 逐渐增大 | B. | 逐渐变小 | C. | 不变 | D. | 先增大,后变小 |
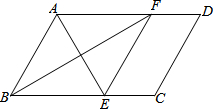 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.