Question

4．如图，O₁O₂=R，以O₁，O₂为圆心，R为半径作圆，正方形ABCD内接于两圆的公共部分，求ABCD的面积．

Answer 1

分析 连接EF交AD于H，交O₁O₂于O，连接EO₁，EO₂，设正方形的边长为x，根据等边三角形的性质表示出EO，根据相似三角形的性质得到比例式，代入计算即可．

解答 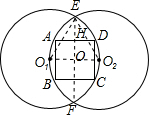解：连接EF交AD于H，交O₁O₂于O，连接EO₁，EO₂，
设正方形的边长为x，
由题意得△EO₁O₂为等边三角形，
∴EO=$\frac{\sqrt{3}}{2}$R，
∵AD∥O₁O₂，
∴$\frac{x}{R}$=$\frac{\frac{\sqrt{3}}{2}R-\frac{x}{2}}{\frac{\sqrt{3}}{2}R}$，
解得x=$\frac{3-\sqrt{3}}{2}$．
则ABCD的面积=x²=$\frac{6-3\sqrt{3}}{2}$．

点评 本题考查的是相交两圆的性质和正方形的性质，掌握相交两圆的连心线垂直平分公共弦是解题的关键，注意相似三角形的性质的运用．