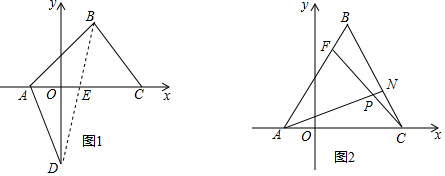题目内容
8. 如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )
如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )| A. | 120° | B. | 130° | C. | 150° | D. | 90° |
分析 先根据OC⊥OA,∠BOC=30°,即可得出∠AOB=90°-30°=60°,再根据OB⊥OD,即可得到∠AOD的度数.
解答 解:∵OC⊥OA,∠BOC=30°,
∴∠AOB=90°-30°=60°,
又∵OB⊥OD,
∴∠AOD=∠AOB+∠BOD=60°+90°=150°,
故选:C.
点评 本题主要考查了余角与补角,解题时注意:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.

练习册系列答案
相关题目
13.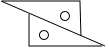 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 以上都不对 |
17.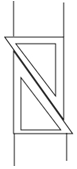 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )| A. | 同位角相等,两直线平行 | B. | 同旁内角互补,两直线平行 | ||
| C. | 平行于同一条直线的两直线平行 | D. | 内错角相等,两直线平行 |
 如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.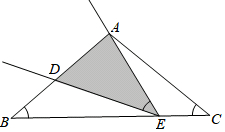 如图,在等腰△ABC中,AB=AC=8cm,BC=10cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.
如图,在等腰△ABC中,AB=AC=8cm,BC=10cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.