题目内容
2. 如图,在Rt△ABC中,∠C=90°,∠A=$\frac{1}{2}$∠ABC,BC平分∠ABC,DE⊥AB,CD=4cm,求AB的长.
如图,在Rt△ABC中,∠C=90°,∠A=$\frac{1}{2}$∠ABC,BC平分∠ABC,DE⊥AB,CD=4cm,求AB的长.
分析 根据直角三角形的性质得到∠A=30°,∠ABC=60°,根据角平分线的定义得到∠DBE=30°,根据角平分线的性质得到DE=CD=4cm,解直角三角形即可得到结论.
解答 解:∵∠C=90°,∠A=$\frac{1}{2}$∠ABC,
∴∠A=30°,∠ABC=60°,
∵BC平分∠ABC,
∴∠DBE=30°,
∴∠A=∠DBE,
∴BD=AD,
∵DE⊥AB,CD=4cm,
∴DE=CD=4cm,
∴AE=BE=$\sqrt{3}$DE=4$\sqrt{3}$,
∴AB=8$\sqrt{3}$,
故答案为:8$\sqrt{3}$.
点评 本题考查了角平分线的性质,直角三角形的性质,熟练掌握角平分线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.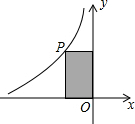 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
14.已知2a=3b(ab≠0),则下列比例式成立的是( )
| A. | $\frac{a}{2}$=$\frac{3}{b}$ | B. | $\frac{a}{3}$=$\frac{b}{2}$ | C. | $\frac{a}{b}$=$\frac{2}{3}$ | D. | $\frac{b}{a}$=$\frac{3}{2}$ |
14.因式分解x3-2x2+x正确的是( )
| A. | (x-1)2 | B. | x (x-1)2 | C. | x( x2-2x+1) | D. | x (x+1)2 |
15.已知甲、乙两数的和是6,甲数是乙数的3倍,设甲数为x,乙数为y,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=6}\\{x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6}\\{y=3x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=6}\\{x=3y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{y=3x}\end{array}\right.$ |
 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )