题目内容
 如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,
如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,(1)求∠BCD的度数;
(2)求四边形ABCD的面积.
考点:全等三角形的判定与性质,垂径定理,圆周角定理
专题:
分析:(1)根据圆内接四边的性质对角互补可直接得出答案;
(2)根据AC是⊙O的直径,得出∠ABC=∠D=90°,利用HL得出Rt△ABC≌Rt△ADC,从而得出∠BAC=∠DAC=
∠BAD=15°,连接OB,得出∠ABO=∠BAC,∠BOC=∠ABO+∠BAC根据AC的长,求出OB的长,过点B作BE⊥AC于E,求出BE,根据三角形的面积公式得出S△ABC,从而求出S△ADC=S△ABC,最后根据四边形ABCD的面积=S△ABC+S△ACD即可得出答案.
(2)根据AC是⊙O的直径,得出∠ABC=∠D=90°,利用HL得出Rt△ABC≌Rt△ADC,从而得出∠BAC=∠DAC=
| 1 |
| 2 |
解答:解:(1)∵∠BAD=30°,
∴∠BAD=180°-30°=150°;
(2)∵AC是⊙O的直径,
∴∠ABC=∠D=90°,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC=
∠BAD=
×30°=15°,
连接OB,则OA=OB,
∴∠ABO=∠BAC=15°,
∴∠BOC=∠ABO+∠BAC=15°+15°=30°,
∵AC=4,
∴OB=OA=
AC=
×4=2,
过点B作BE⊥AC于E,
则BE=
OB=
×2=1,
∴S△ABC=
AC•BE=
×4×1=2,
∵Rt△ABC≌Rt△ADC,∴S△ADC=S△ABC=2,
四边形ABCD的面积=S△ABC+S△ACD=2+2=4.
∴∠BAD=180°-30°=150°;
(2)∵AC是⊙O的直径,
∴∠ABC=∠D=90°,
在Rt△ABC和Rt△ADC中,
|
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC=
| 1 |
| 2 |
| 1 |
| 2 |
连接OB,则OA=OB,
∴∠ABO=∠BAC=15°,
∴∠BOC=∠ABO+∠BAC=15°+15°=30°,

∵AC=4,
∴OB=OA=
| 1 |
| 2 |
| 1 |
| 2 |
过点B作BE⊥AC于E,
则BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵Rt△ABC≌Rt△ADC,∴S△ADC=S△ABC=2,
四边形ABCD的面积=S△ABC+S△ACD=2+2=4.
点评:此题考查了全等三角形的判定与性质,用到的知识点是圆内接四边的性质、垂径定理、圆周角定理、三角形的面积公式等,关键是根据题意做出辅助线构造出直角三角形.

练习册系列答案
相关题目
 某学习小组想了解南京市“迎青奥”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.
某学习小组想了解南京市“迎青奥”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.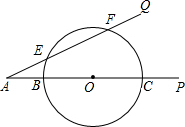 已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求: 某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.
某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支. 如图,在图1中,AB是圆的直径,点P是根据圆的相关性质用无刻度的直尺画出的△ABC三条高的交点;依据图1给你的作法启示,请你在图2中,先用尺规画出以AB为直径的⊙0,然后仅用无刻度的直尺画出△ABC中AB边上的高CD.(要求:不写作法,保留作图痕迹,写出结论.)
如图,在图1中,AB是圆的直径,点P是根据圆的相关性质用无刻度的直尺画出的△ABC三条高的交点;依据图1给你的作法启示,请你在图2中,先用尺规画出以AB为直径的⊙0,然后仅用无刻度的直尺画出△ABC中AB边上的高CD.(要求:不写作法,保留作图痕迹,写出结论.) 某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=
某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=
 如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为10cm,则四边形EFGH的周长是
如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为10cm,则四边形EFGH的周长是