题目内容
用适当的方法解下列方程:
(1)x2-2x-9=0;
(2)(5x-3)2+2(3-5x)=0.
(1)x2-2x-9=0;
(2)(5x-3)2+2(3-5x)=0.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)用公式法求解即可;
(2)先变形,再提公因式,求解即可.
(2)先变形,再提公因式,求解即可.
解答:解:(1)a=1,b=-2,c=-9,
△=b2-4ac=4+36=40>0,有两个不相等的实数根,
x=
=
=1±
,
x1=1+
,x2=1-
;
(2)原方程变形为:(5x-3)2-2(5x-3)=0,
(5x-3)(5x-3-2)=0,
5x-3=0,5x-5=0,
x1=
,x2=1.
△=b2-4ac=4+36=40>0,有两个不相等的实数根,
x=
-b±
| ||
| 2a |
2±
| ||
| 2 |
| 10 |
x1=1+
| 10 |
| 10 |
(2)原方程变形为:(5x-3)2-2(5x-3)=0,
(5x-3)(5x-3-2)=0,
5x-3=0,5x-5=0,
x1=
| 3 |
| 5 |
点评:本题考查了解一元二次方程的方法--因式分解,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
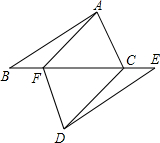 如图,已知△ABF≌△DEC,且AC=DF,说明△ABC≌△DEF的理由.
如图,已知△ABF≌△DEC,且AC=DF,说明△ABC≌△DEF的理由.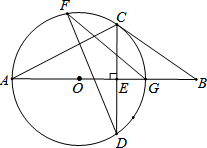 如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.