题目内容
18. 实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.
实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.
分析 设AM=x,根据AM2=BM•AB列一元二次方程,求出x,得出AM=BN=$\sqrt{5}$-1,从而求出MN的长,即m-n的长.
解答 解:由题意得:AB=b-a=2
设AM=x,则BM=2-x
x2=2(2-x)
x=-1±$\sqrt{5}$
x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$(舍)
则AM=BN=$\sqrt{5}$-1
∴MN=m-n=AM+BN-2=2($\sqrt{5}$-1)-2=2$\sqrt{5}$-4
故答案为:2$\sqrt{5}$-4.
点评 本题考查了数轴上两点的距离和黄金分割的定义及一元二次方程,做好此题的关键是能正确表示数轴上两点的距离:若A表示xA、B表示xB,则AB=|xB-xA|;同时会用配方法解一元二次方程,理解线段的和、差关系.

练习册系列答案
相关题目
10.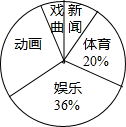 为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;
(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
 为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)| 节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
| 人数 | 36 | 90 | a | b | 27 |
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;
(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
 三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°.
三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:
 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
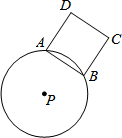 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π. 如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为5.
如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为5.