题目内容
如图,已知反比例函数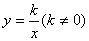 的图象经过点(
的图象经过点(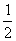 ,8),直线
,8),直线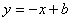 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4,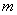 ).
).

(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 轴、
轴、 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
(1) ,
, ;
; .
.
【解析】(1)由反比例函数的图象经过点(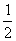 ,8),可知
,8),可知 ,所以反比例函数解析式为
,所以反比例函数解析式为 ,∵点Q是反比例函数和直线
,∵点Q是反比例函数和直线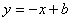 的交点,∴
的交点,∴ ,∴点Q的坐标是(4,1),∴
,∴点Q的坐标是(4,1),∴ ,∴直线的解析式为
,∴直线的解析式为 .
.
(2)如图所示:由直线的解析式 可知与
可知与 轴和
轴和 轴交点坐标点A与点B的坐标分别为(5,0)、(0,5),由反比例函数与直线的解析式:
轴交点坐标点A与点B的坐标分别为(5,0)、(0,5),由反比例函数与直线的解析式: ,
,
可知两图像的交点坐标分别点P(1,4)和点Q(4,1),过点P作PC⊥ 轴,垂足为C,过点Q作QD⊥
轴,垂足为C,过点Q作QD⊥ 轴,垂足为D,
轴,垂足为D,
∴S△OPQ=S△AOB-S△OAQ-S△OBP =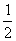 ×OA×OB-
×OA×OB-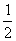 ×OA×QD-
×OA×QD-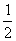 ×OB×PC
×OB×PC
=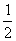 ×25-
×25-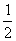 ×5×1-
×5×1-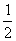 ×5×1=
×5×1= .
.

练习册系列答案
相关题目
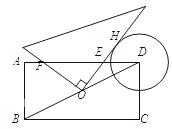
 ABCD中,AB=
ABCD中,AB= ,延长BC至E,使BE=BD,则△BDE的面积为 。
,延长BC至E,使BE=BD,则△BDE的面积为 。
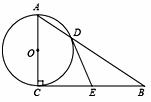
 的圆心O在格点上,则∠AED的正切值等于_______________.
的圆心O在格点上,则∠AED的正切值等于_______________.
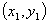 ,B
,B ,AB中点P的坐标为
,AB中点P的坐标为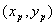 .由
.由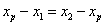 ,得
,得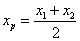 ,同理
,同理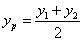 ,所以AB的中点坐标为(
,所以AB的中点坐标为(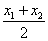 ,
, ).由勾股定理得
).由勾股定理得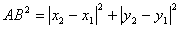 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=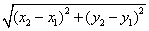 .
. 与抛物线
与抛物线 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.



 (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;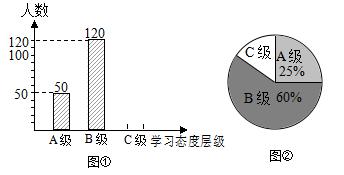
 向B地,
向B地, 甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.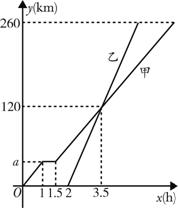


 数表达式
数表达式 ,并写出相应
,并写出相应