题目内容
20.某汽车销售公司2月份销售某厂汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出1辆汽车,则该辆汽车的进价为30万元;每多售出1辆,所有售出的汽车的进价均降低0.1万元.月底厂家一次性返利给销售公司,每辆返利0.5万元.
(1)若该公司当月售出7辆汽车,则每辆汽车的进价为多少万元?
(2)如果汽车的售价为每辆31万元,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
分析 (1)根据若当月仅售出1辆汽车,则该辆汽车的进价为30万元,每多售出1辆,所有售出的汽车的进价均降低0.1万元/辆,得出该公司当月售出7辆汽车时,则每辆汽车的进价为:30-0.1×(7-1),即可得出答案;
(2)利用设需要售出x辆汽车,由题意可知,每辆汽车的销售利润,列出一元二次方程.
解答 解:(1)若该公司当月售出7辆汽车,则每辆汽车的进价为:30-0.1×(7-1)=29.4万元
(2)设需要售出x辆汽车,
由题意可知,每辆汽车的销售利润为:
[31-(30.1-0.1x)]x+0.5x=12,
整理,得x2+14x-120=0,
解这个方程,得x1=-20(不合题意,舍去),x2=6.
答:需要售出6辆汽车.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系并进行分段讨论是解题关键.

练习册系列答案
相关题目
10.下列说法不正确的是( )
| A. | (-$\frac{1}{4}$)2的平方根是±$\frac{1}{4}$ | B. | 0.9的算术平方根是0.3 | ||
| C. | -5是25的一个平方根 | D. | $\root{3}{-27}$=-3 |
11.甲打360个字与乙打480个字所用时间相同,已知两人每分钟共打140个字.若设甲每分钟打x个字,则可列方程( )
| A. | $\frac{360}{x}$=$\frac{480}{140-x}$ | B. | $\frac{480}{x}$=$\frac{360}{140-x}$ | C. | $\frac{360}{x}$+$\frac{480}{x}$=140 | D. | x+$\frac{360x}{480}$=140 |
5. 如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
 如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )| A. | $\sqrt{74}$ | B. | $\sqrt{74}$+3 | C. | $\sqrt{74}$-3 | D. | 3 |
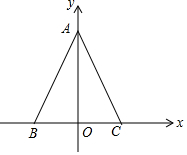 如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).
如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0). 如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:AB⊥GD.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:AB⊥GD.