Question

将一副三角尺叠放在一起：
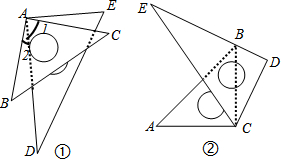
（1）如图①，在此种图案的情形下，若∠1=3∠2，请计算出∠CAE的度数；
（2）如图②，在此种图案的情形下，能否使∠ACE=2∠BCD？若能，请求出∠ACD；若不能，请说明理由．

Answer 1

考点：角的计算,余角和补角

专题：

分析：（1）求出∠2=∠CAE，根据∠1=3∠2，∠1+∠2=90°求出∠2即可；
（2）设∠BCD=x°，则∠ACE=2x°，根据∠ECB+∠DCB=60°得出90-2x+x=60，求出x即可．

解答：解：（1）∵∠CAE+∠1=90°，∠2+∠1=90°，
∴∠CAE=∠2，
∵∠1=3∠2，∠1+∠2=90°，
∴∠2=22.5°，
∴∠CAE的度数是22.5°；

（2）能，
理由是：设∠BCD=x°，则∠ACE=2x°，
∵∠ECB+∠DCB=60°，
∴90-2x+x=60，
x=30，
即∠BCD=30°，
∴∠ACD=90°+30°=120°，
即能使∠ACE=2∠BCD，此时∠ACD=120°．

点评：本题考查了互余、互补，角的有关计算的应用，主要考查学生的计算能力，题目比较好，难度适中．