题目内容
3.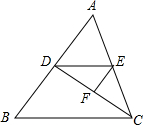 如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.(1)求证:∠AED=∠ACB;
(2)若D、E、F分别是AB、AC、CD边上的中点,S四边形ADFE=9,求S△ABC.
分析 (1)由BDC+∠EFC=180°和∠EFC+∠DFE=180°得到∠BDC=∠DFE,根据平行线的判定得AB∥EF,则∠ADE=∠DEF,而∠DEF=∠B,所以∠ADE=∠B,于是可判断DE∥BC,然后根据平行线的性质得到∠AED=∠ACB;
(2)由E为AC的中点,根据三角形面积公式得到S△ADE=S△CDE=$\frac{1}{2}$S△ADC,再由F为DC的中点得S△DEF=S△CEF=$\frac{1}{2}$S△DEC,而S四边形ADFE=9,则S△ADE+$\frac{1}{2}$S△EDC=9,可计算出S△ADE=6,则S△ADC=12,然后利用D为AB的中点,根据S△ABC=2S△ADC进行计算即可.
解答  (1)证明:∵∠BDC+∠EFC=180°(已知),
(1)证明:∵∠BDC+∠EFC=180°(已知),
而∠EFC+∠DFE=180°(邻补角的定义),
∴∠BDC=∠DFE(等角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠ADE=∠DEF(两直线平行,内错角相等),
∵∠DEF=∠B(已知),
∴∠ADE=∠B(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB(两直线平行,同位角相等);
(2)解:∵E为AC的中点,
∴S△ADE=S△CDE=$\frac{1}{2}$S△ADC,
∵F为DC的中点,
∴S△DEF=S△CEF=$\frac{1}{2}$S△DEC,
∵S四边形ADFE=9,
∴S△ADE+$\frac{1}{2}$S△EDC=9,
∴$\frac{3}{2}$S△ADE=9,
∴S△ADE=6,
∴S△ADC=2×6=12,
∵D为AB的中点,
∴S△ABC=2S△ADC=2×12=24.
点评 本题考查了行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系;应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.也考查了三角形面积公式.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | 不大于8 | B. | 大于8小于9 | C. | 大于9小于12 | D. | 总是8 |
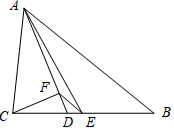 如图,△ABC中,AB=4,AC=2,AD、AE分别是其角平分线和中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为( )
如图,△ABC中,AB=4,AC=2,AD、AE分别是其角平分线和中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
| A. | m≠1 | B. | m<0 | C. | m>1 | D. | m<1 |
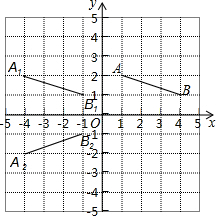 如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1),
如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1), 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P2017的坐标是(672,1).
如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P2017的坐标是(672,1). 已知点O是直线AB上的点,∠COA=∠DOB=35°.
已知点O是直线AB上的点,∠COA=∠DOB=35°.