题目内容
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=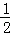 BC,连接CD和EF.
BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
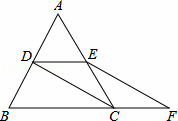
(1)证明:∵D、E分别为AB、AC的中点,
∴DE
 BC,
BC,
∵延长BC至点F,使CF= BC,
BC,
∴DE FC,
FC,
即DE=CF;
(2)解:∵DE FC,
FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF= .
.


练习册系列答案
相关题目
某校篮球队五名主力队员的身高分别是174,179,180,174,178(单位:cm),则这五名队员身高的中位数是( )
|
| A. | 174cm | B. | 177cm | C. | 178cm | D. | 180cm |
如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )

|
| A. |
| B. |
| C. |
| D. |
|
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )

|
| A. | 由小到大 | B. | 由大到小 |
|
| C. | 不变 | D. | 先由小到大,后由大到小 |
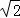 ≈1.41,
≈1.41,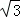 ≈1.73)
≈1.73)




 (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点. k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=
k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn= ,求n的值.
,求n的值.
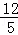 ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D ,使四边形ABCD为对等四边形,并求出CD的长.
,使四边形ABCD为对等四边形,并求出CD的长.