题目内容
如图,已知直线y=x+k和双曲线y= (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当 k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=
k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn= ,求n的值.
,求n的值.

解:(1)当k=1时,直线y=x+k和双曲线y= 化为:y=x+1和y=
化为:y=x+1和y= ,
,
解 得
得 ,
, ,
,
∴A(1,2),B(﹣2,﹣1),
(2)当k=2时,直线y=x+k和双曲线y= 化为:y=x+2和y=
化为:y=x+2和y= ,
,
解 得
得 ,
, ,
,
∴A(1,3),B(﹣3,﹣1)
设直线AB的解析式为:y=mx+n,
∴
∴ ,
,
∴直线AB的解析式为:y=x+2
∴直线AB与y轴的交点(0,2),
∴S△AOB= ×2×1+
×2×1+ ×2×3=4;
×2×3=4;
(3)当k=1时,S1= ×1×(1+2)=
×1×(1+2)= ,
,
当k=2时,S2= ×2×(1+3)=4,
×2×(1+3)=4,
…
当k=n时,Sn= n(1+n+1)=
n(1+n+1)= n2+n,
n2+n,
∵S1+S2+…+Sn= ,
,
∴ ×(
×( …+n2)+(1+2+3+…n)=
…+n2)+(1+2+3+…n)= ,
,
整理得: ,
,
 解得:n=6.
解得:n=6.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
下列运算正确的是( )
|
| A. | a6÷a2=a3 | B. | (a+b)2=a2+b2 | C. | 2﹣3=﹣6 | D. |
|
某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
|
| A. | 众数是35 | B. | 中位数是34 | C. | 平均数是35 | D. | 方差是6 |
 ,b2+1=
,b2+1= ,则2015|a﹣b|=
,则2015|a﹣b|= 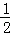 BC,连接CD和EF.
BC,连接CD和EF.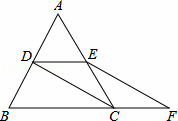
 =﹣3
=﹣3 ,则x2﹣y2的值为
,则x2﹣y2的值为  的方程
的方程 的两根之和为
的两根之和为 ,两根之差为1,其中
,两根之差为1,其中 是△
是△ 的三边长.
的三边长.