题目内容
 如图所示将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠EFG=50°,则∠BGE的度数为
如图所示将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠EFG=50°,则∠BGE的度数为考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:利用翻折的性质,得∠DEF=∠GEF;然后根据两直线平行,内错角相等,求得∠BGE=∠DEG,∠DEF=∠EFG;最后由等量代换求得∠BGE的度数.
解答:解:根据翻折的性质,得
∠DEF=∠GEF;
∵AD∥BC,
∴∠DEF=∠EFG(两直线平行,内错角相等);
∠BGE=∠DEG(两直线平行,内错角相等);
∵∠EFG=50°,
∴∠BGE=2∠EFG=100°.
故答案为:100°.
∠DEF=∠GEF;
∵AD∥BC,
∴∠DEF=∠EFG(两直线平行,内错角相等);
∠BGE=∠DEG(两直线平行,内错角相等);
∵∠EFG=50°,
∴∠BGE=2∠EFG=100°.
故答案为:100°.
点评:本题考查了平行线的性质、翻折变换(折叠问题).正确观察图形,熟练掌握平行线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若a、b、c为△ABC的三边,那么关于代数式(a-b)2-c2的值,以下判断正确的是( )
| A、大于0 | B、等于0 |
| C、小于0 | D、以上均有可能 |
下列方程组中,二元一次方程组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是( )
如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是( )A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
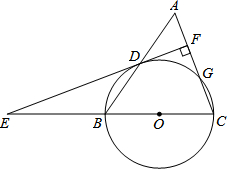 如图,等腰三角形ABC中,AC=BC=6,AB=8.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=6,AB=8.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 已知:正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M.
已知:正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M. 如图,P是∠ABC的边BC上一点,sin∠ABC=
如图,P是∠ABC的边BC上一点,sin∠ABC= 如图,AB∥CD,∠A=70°,则∠COE=
如图,AB∥CD,∠A=70°,则∠COE=