题目内容
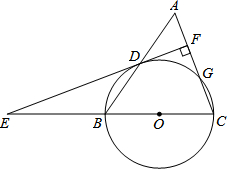 如图,等腰三角形ABC中,AC=BC=6,AB=8.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=6,AB=8.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.(1)求证:直线EF是⊙O的切线;
(2)求sin∠E的值.
(3)求ED的长.
考点:切线的判定,勾股定理,解直角三角形
专题:
分析:(1)先连结OD,CD,由于AC=BC,得出D是AB的中点.由O是BC的中点,得出DO∥AC,可证EF是⊙O的切线;
(2)连接BG,可得BG∥EF,那么∠E=∠GBC,都表示出BG2,利用勾股定理求得CG的值,CG:BC即为sinE的值;
(3)利用(2)中所求得出sin∠E=
=
,求出EO的长,再利用勾股定理求出DE的长.
(2)连接BG,可得BG∥EF,那么∠E=∠GBC,都表示出BG2,利用勾股定理求得CG的值,CG:BC即为sinE的值;
(3)利用(2)中所求得出sin∠E=
| OD |
| OE |
| 1 |
| 9 |
解答:(1)证明:如图,连结OD,CD,则∠BDC=90°.
∴CD⊥AB.
∵AC=BC,∴AD=BD.
∴D是AB的中点.
∵O是BC的中点,
∴DO∥AC.
∵EF⊥AC于F.
∴EF⊥DO.
∴EF是⊙O的切线.

( 2 )解:连结BG,
∵BC是直径,∴∠BGC=90°=∠CFE.
∴BG∥EF.
∴sin∠E=
=
.
设CG=x,则AG=6-x.
在Rt△BGA中,BG2=BC2-CG2.
在Rt△BGC中,BG2=BA2-AG2.
∴62-x2=82-(6-x)2.
解得:x=
.即CG=
.
在Rt△BGC中.
∴sin∠E=
=
=
.
(3)解:由题意和(2)可得,OD=3
在Rt△ODE中
sin∠E=
=
,
∴OE=27,
∴DE=
=12
.
∴CD⊥AB.
∵AC=BC,∴AD=BD.
∴D是AB的中点.
∵O是BC的中点,
∴DO∥AC.
∵EF⊥AC于F.
∴EF⊥DO.
∴EF是⊙O的切线.

( 2 )解:连结BG,
∵BC是直径,∴∠BGC=90°=∠CFE.
∴BG∥EF.
∴sin∠E=
| FC |
| EC |
| CG |
| BC |
设CG=x,则AG=6-x.
在Rt△BGA中,BG2=BC2-CG2.
在Rt△BGC中,BG2=BA2-AG2.
∴62-x2=82-(6-x)2.
解得:x=
| 2 |
| 3 |
| 2 |
| 3 |
在Rt△BGC中.
∴sin∠E=
| CG |
| BC |
| ||
| 6 |
| 1 |
| 9 |
(3)解:由题意和(2)可得,OD=3
在Rt△ODE中
sin∠E=
| OD |
| OE |
| 1 |
| 9 |
∴OE=27,
∴DE=
| 272-32 |
| 5 |
点评:本题考查了切线的判定、等腰三角形的性质、平行线的判定和性质及勾股定理的应用;把所求角进行转移是基本思路,求得CG的长是解决本题的难点.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
不等式组
的解集为( )
|
A、 |
B、 |
C、 |
D、 |
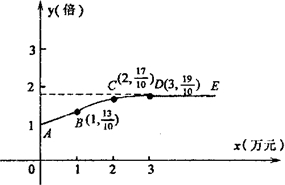 某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系
某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系
 如图所示将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠EFG=50°,则∠BGE的度数为
如图所示将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠EFG=50°,则∠BGE的度数为