题目内容
若a、b、c为△ABC的三边，那么关于代数式（a-b）2-c2的值，以下判断正确的是（ ）
| A、大于0 | B、等于0 |
| C、小于0 | D、以上均有可能 |
考点：因式分解的应用,三角形三边关系
专题：
分析：根据三角形中任意两边之和大于第三边．把代数式（a-b）2-c2分解因式就可以进行判断．
解答：解：（a-b）2-c2=（a+c-b）[a-（b+c）]．
∵a，b，c是三角形的三边．
∴a+c-b＞0，a-（b+c）＜0．
∴（a-b）2-c2＜0．
故选C．
∵a，b，c是三角形的三边．
∴a+c-b＞0，a-（b+c）＜0．
∴（a-b）2-c2＜0．
故选C．
点评：本题考查了三角形中三边之间的关系．（a+c-b）[a-（b+c）]是一个正数与负数的积，所以小于0．
练习册系列答案
同步练习强化拓展系列答案
相关题目
如图，在△ABC中，AB=AC，∠A=100°，M、N、P分别是AB、AC、BC边上一点，且BM=BP，CN=CP，则∠MPN的度数为如下图所示的圆均为半径为1的等圆，且相邻两圆外切，圆心连线构成正三角形，记各阴影部分面积从左到右依次为S1、S2、S3、…，Sn，则S10=（ ）
| A、13π | ||
B、
| ||
| C、16π | ||
D、
|
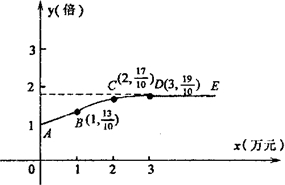某公司生产一种产品，每件成本3元，售价4元，年销售量20万件，为获得更好的效益，公司准备拿出一定资金做广告．根据经验，设广告费x万元，做广告后的年销售量是原销售量的y倍，且y与x的关系
如图所示将一张长方形纸条ABCD沿EF折叠后，ED与BF交于G点，若∠EFG=50°，则∠BGE的度数为