题目内容
在Rt△ABC中,∠C=90°,BC=3,AC=4,以点B为圆心,以2为半径作圆,P是AC上的一个动点,过点P作⊙B的一条切线,切点为Q.
(1)如图1,连接BP,BQ,当点P是AC的中点时,求证:△PBQ≌△BPC;
(2)如图2,求PQ的最小值,并确定此时点P的位置.
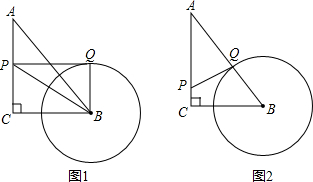
(1)如图1,连接BP,BQ,当点P是AC的中点时,求证:△PBQ≌△BPC;
(2)如图2,求PQ的最小值,并确定此时点P的位置.

考点:切线的性质,全等三角形的判定与性质
专题:
分析:(1)根据切线的性质求得∠PQB=90°,然后根据已知求得PC=BQ=2,根据HL即可求得△PBQ≌△BPC;
(2)当P移动到C位置时,PQ的值最小,根据勾股定理即可求得PQ的最小值,从而确定P的位置.
(2)当P移动到C位置时,PQ的值最小,根据勾股定理即可求得PQ的最小值,从而确定P的位置.
解答:解:(1)∵PQ是⊙B的切线,
∴BQ⊥PQ,
∴∠PQB=90°,
∵AC=4,点P是AC的中点,
∴PC=2,
∵BQ=2,
∴PC=BQ,
在RT△PBC和RT△BPQ中,
,
∴RT△PBC≌RT△BPQ(HL),
即△PBQ≌△BPC;
(2)过C点作⊙B的切线CQ′,连接BQ′,
∴BQ′⊥CQ′,
∵BC=3,BQ′=2,
∴CQ′=
=
,
∴当P处于C位置时,PQ的值最小,最小值为
.
∴BQ⊥PQ,
∴∠PQB=90°,
∵AC=4,点P是AC的中点,
∴PC=2,
∵BQ=2,
∴PC=BQ,
在RT△PBC和RT△BPQ中,
|
∴RT△PBC≌RT△BPQ(HL),
即△PBQ≌△BPC;
(2)过C点作⊙B的切线CQ′,连接BQ′,
∴BQ′⊥CQ′,
∵BC=3,BQ′=2,
∴CQ′=
| 32-22 |
| 5 |
∴当P处于C位置时,PQ的值最小,最小值为
| 5 |
点评:本题考查 了切线的性质,全等三角形的判定和性质,勾股定理的应用等,熟练掌握切线的性质以及三角形全等的判定是本题的关键.

练习册系列答案
相关题目
 如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是
如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是 如图,AC为⊙O的直径,B,D为⊙O上的两点,则由A,B,C,D,四点可以构造
如图,AC为⊙O的直径,B,D为⊙O上的两点,则由A,B,C,D,四点可以构造 如图,△ABC中,D是AB的中点,AC=12,BC=5,CD=
如图,△ABC中,D是AB的中点,AC=12,BC=5,CD=