题目内容
11．
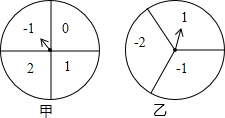如图，甲、乙分别是4等分、3等分的两个圆转盘，指针固定，转盘转动停止后，指针指向某一数字．（1）直接写出转动甲盘停止后指针指向数字“1”的概率；
（2）小华和小明利用这两个转盘做游戏，两人分别同时转动甲、乙两个转盘，停止后，指针各指向一个数字，若两数字之积为非负数则小华胜；否则，小明胜．你认为这个游戏公平吗？请你利用列举法说明理由．
分析 （1）由题意可知转盘中共有四个数，其中“1”只有一种，进而求出其概率；
（2）首先根据题意列出表格，然后由表格即可求得所有等可能的结果与小华、小明获胜的情况，继而求得小华、小明获胜的概率，比较概率大小，即可知这个游戏是否公平．
解答 解：（1）甲盘停止后指针指向数字“1”的概率=$\frac{1}{4}$；
（2）列表得：
转盘A 两个数字之积 转盘B | -1 | 0 | 2 | 1 |
| 1 | -1 | 0 | 2 | 1 |
| -2 | 2 | 0 | -4 | -2 |
| -1 | 1 | 0 | -2 | -1 |
∴P（小华获胜）=$\frac{7}{12}$，P（小明获胜）=$\frac{5}{12}$．
∴这个游戏对双方不公平．
点评 本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．
练习册系列答案
阅读快车系列答案
相关题目
如图，平面展开图折叠成正方体后，相对面上的两个代数式值相等，则x+y=5．
6．抛物线y=-$\frac{1}{3}$（x-5）2+3的对称轴是（ ）
| A． | 直线x=-$\frac{1}{3}$ | B． | 直线x=-5 | C． | 直线x=3 | D． | 直线x=5 |
某小区有两段长度相等的道路需硬化，现分别由甲、乙两个工程队同时开始施工，如图的线段和折线是两对前6天硬化的道路长y甲、y乙（米）与施工时间x（天）之间的函数图象．
3．寒假即将来临，小明要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动，那么小明选择到甲社区参加实践活动的可能性为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{9}$ |