题目内容
6.抛物线y=-$\frac{1}{3}$(x-5)2+3的对称轴是( )| A. | 直线x=-$\frac{1}{3}$ | B. | 直线x=-5 | C. | 直线x=3 | D. | 直线x=5 |
分析 根据二次函数的性质对各选项进行判断.
解答 解:二次函数y=-$\frac{1}{3}$(x-5)2+3的对称轴为直线x=5.
故选D.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
17.某商店对于某个商品的销售量与获利做了统计,得到下表:
若获利是销售量的二次函数,那么,该商店获利的最大值是( )
| 销售量(件) | 100 | 200 | 300 |
| 获利(万元) | 7 | 9 | 9 |
| A. | 9万元 | B. | 9.25万元 | C. | 9.5万元 | D. | 10万元 |
14. 如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )
如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )
(1)AE=CD;(2)BP=BQ;(3)PQ∥AD;(4)CQ=CA;(5)EP=QD.
 如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )
如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )(1)AE=CD;(2)BP=BQ;(3)PQ∥AD;(4)CQ=CA;(5)EP=QD.
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
18. 如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
 如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
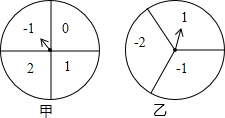 如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.