题目内容
6.(1)算一算:$\sqrt{4}$×$\sqrt{9}$=6,$\sqrt{4×9}$=6;$\sqrt{\frac{9}{25}}$×$\sqrt{25}$=3,$\sqrt{\frac{9}{25}×25}$=3.
(2)想一想:你发现什么了吗,换几个数再试试,是否有相同规律:对于实数a、b,有$\sqrt{a}$×$\sqrt{b}$=$\sqrt{ab}$(a≥0,b≥0).
(3)用一用:运用上述规律求值:①$\sqrt{3.6}$×$\sqrt{10}$=6;②$\sqrt{49×64}$=56.
分析 (1)利用算术平方根的定义计算即可得到结果;
(2)归纳总结得到二次根式乘法法则,写出即可;
(3)利用得出的规律计算即可得到结果.
解答 解:(1)$\sqrt{4}$×$\sqrt{9}$=2×3=6;$\sqrt{4×9}$=$\sqrt{36}$=6;$\sqrt{\frac{9}{25}}$×$\sqrt{25}$=$\frac{3}{5}$×5=3;$\sqrt{\frac{9}{25}×25}$=$\sqrt{9}$=3;
(2)根据题意得:$\sqrt{a}$×$\sqrt{b}$=$\sqrt{ab}$(a≥0,b≥0);
(3)①原式=$\sqrt{36}$=6;②原式=$\sqrt{49}$×$\sqrt{64}$=7×8=56.
故答案为:(1)6;6;3;3;(2)$\sqrt{ab}$;≥;≥;(3)①6;②56.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
14.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )


| A. | 只有(1)相似 | B. | 只有(2)相似 | C. | 都相似 | D. | 都不相似 |
 如图,?ABCD和?EAFC的顶点为D,B,E,F在同一条直线上.求证:DE=BF.
如图,?ABCD和?EAFC的顶点为D,B,E,F在同一条直线上.求证:DE=BF.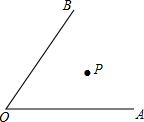 如图,某市的牛奶加工长P恰好在两条铁路OA、OB的夹角内部,为了提高牛奶的销量,经理决定在这两条铁路沿线上各建一个转运站M、N,加工厂的运货车每天从加工厂P向转运站M、N运送成品牛奶,问转运站M、N应建在何处,能够使运货车以最短的路程回到加工厂P?
如图,某市的牛奶加工长P恰好在两条铁路OA、OB的夹角内部,为了提高牛奶的销量,经理决定在这两条铁路沿线上各建一个转运站M、N,加工厂的运货车每天从加工厂P向转运站M、N运送成品牛奶,问转运站M、N应建在何处,能够使运货车以最短的路程回到加工厂P?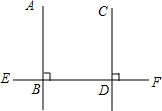 写出下列命题的已知、求证,并完成证明过程.
写出下列命题的已知、求证,并完成证明过程. 已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由.
已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由. 观察探究,完成证明和填空.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.
观察探究,完成证明和填空.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.