Question

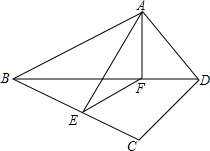
6．如图所示，在△ABC中，D是BC延长线上一点，CD=BC，E是CA延长线上一点，AE=2AC，若AD=BE，求证：△ABC是直角三角形．

Answer 1

分析 由于告诉了AE=2AC，故延长AC至F，使CF=AC，连接BF，则△ADC≌△FBC，从而AD=BF，又AD=BE，从而BF=BE，即三角形BEF是等腰三角形，再根据AE=2AC，可得A是EF中点，由三线合一可得BA垂直EF．

解答 证明：如图，延长AC至F，使CF=AC，连接BF，

∵BC=CD，
在△ADC和△FBC中，
$\left\{\begin{array}{l}{AC=FC}\\{∠ACD=∠FCB}\\{DC=BC}\end{array}\right.$
∴△ADC≌△FBC（SAS），
∴BF=AD，
∵AD=BE，
∴BF=BE，
∵AE=2AC，
∴AE=AF，
∴BA⊥EF，
∴△ABC是直角三角形．

点评 本题主要考查了全等三角形的判定与性质，等腰三角形“三线合一”的性质，难度中等．由题目条件“AE=2AC”联想到中线倍长是解答本题的关键．