题目内容
在△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,5∠C=9∠A,则∠B的度数是________°.
54或68
分析:由5∠C=9∠A,得∠C= ∠A,根据三角形的内角和定理得∠B=180°-∠A-∠C=180°-∠A-
∠A,根据三角形的内角和定理得∠B=180°-∠A-∠C=180°-∠A- ∠A=180°-
∠A=180°- ∠A,而∠A<∠B<∠C,得到不等式组∠A<180°-
∠A,而∠A<∠B<∠C,得到不等式组∠A<180°- ∠A<
∠A< ∠A,解得39
∠A,解得39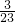 <∠A<47
<∠A<47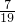 ,而三个内角的度数均为整数,∠C=
,而三个内角的度数均为整数,∠C= ∠A,即可得到∠A=40°或45°,于是就可计算出∠B的度数.
∠A,即可得到∠A=40°或45°,于是就可计算出∠B的度数.
解答:∵5∠C=9∠A,
∴∠C= ∠A,
∠A,
∴∠B=180°-∠A-∠C=180°-∠A- ∠A=180°-
∠A=180°- ∠A,
∠A,
又∵∠A<∠B<∠C,
∴∠A<180°- ∠A<
∠A< ∠A,
∠A,
解此不等式组得,39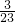 <∠A<47
<∠A<47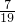 ,
,
而∠A为整数度,所以∠A=40°,41°,42°,43°,44°,45°,46°,47°.
又∵∠C= ∠A,并且∠C为整数度,
∠A,并且∠C为整数度,
∴当∠A=40°时,∠C=72°;
当∠A=45°时,∠C=81°.
所以∠B=180°-40°-72°=68°或∠B=180°-45°-81°=54°.
故答案为54或68.
点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.同时考查了不等式组的解法以及它的整数解.
分析:由5∠C=9∠A,得∠C=
 ∠A,根据三角形的内角和定理得∠B=180°-∠A-∠C=180°-∠A-
∠A,根据三角形的内角和定理得∠B=180°-∠A-∠C=180°-∠A- ∠A=180°-
∠A=180°- ∠A,而∠A<∠B<∠C,得到不等式组∠A<180°-
∠A,而∠A<∠B<∠C,得到不等式组∠A<180°- ∠A<
∠A< ∠A,解得39
∠A,解得39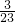 <∠A<47
<∠A<47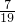 ,而三个内角的度数均为整数,∠C=
,而三个内角的度数均为整数,∠C= ∠A,即可得到∠A=40°或45°,于是就可计算出∠B的度数.
∠A,即可得到∠A=40°或45°,于是就可计算出∠B的度数.解答:∵5∠C=9∠A,
∴∠C=
 ∠A,
∠A,∴∠B=180°-∠A-∠C=180°-∠A-
 ∠A=180°-
∠A=180°- ∠A,
∠A,又∵∠A<∠B<∠C,
∴∠A<180°-
 ∠A<
∠A< ∠A,
∠A,解此不等式组得,39
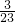 <∠A<47
<∠A<47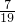 ,
,而∠A为整数度,所以∠A=40°,41°,42°,43°,44°,45°,46°,47°.
又∵∠C=
 ∠A,并且∠C为整数度,
∠A,并且∠C为整数度,∴当∠A=40°时,∠C=72°;
当∠A=45°时,∠C=81°.
所以∠B=180°-40°-72°=68°或∠B=180°-45°-81°=54°.
故答案为54或68.
点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.同时考查了不等式组的解法以及它的整数解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
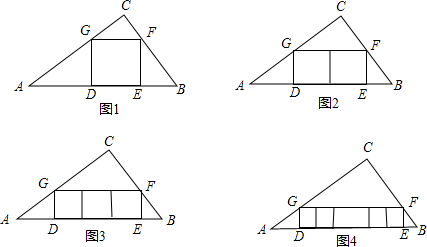


 如图,在△ABC中,AB=AC=
如图,在△ABC中,AB=AC= (1)如图,若在△ABC中有三个内接正方形,其边长分别为a=7,b=5,c=2.试证明∠ACB为直角.
(1)如图,若在△ABC中有三个内接正方形,其边长分别为a=7,b=5,c=2.试证明∠ACB为直角.