题目内容
设m>n>0,m2+n2=6mn,则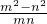 =
=
- A.

- B.

- C.

- D.4
A
分析:对所求式分子进行因式分解,可成为(m+n)(m-n),求出m+n和m-n的值,然后求出解即可.
解答:∵m2+n2=6mn,
∴(m-n)2=4mn,
∵m>n>0,
∴m-n=2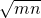 .
.
∵m2+n2=6mn,
∴(m+n)2=8mn.
∵m>n>0,
∴m+n=2 .
.
∴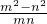 =
= =4
=4 .
.
故选A.
点评:本题考查代数式求值,关键熟悉配方法和完全平方公式,以及平方差公式的应用.
分析:对所求式分子进行因式分解,可成为(m+n)(m-n),求出m+n和m-n的值,然后求出解即可.
解答:∵m2+n2=6mn,
∴(m-n)2=4mn,
∵m>n>0,
∴m-n=2
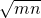 .
.∵m2+n2=6mn,
∴(m+n)2=8mn.
∵m>n>0,
∴m+n=2
 .
.∴
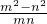 =
= =4
=4 .
.故选A.
点评:本题考查代数式求值,关键熟悉配方法和完全平方公式,以及平方差公式的应用.

练习册系列答案
相关题目
设m>n>0,m2+n2=4mn,则
=( )
| m2-n2 |
| mn |
A、2
| ||
B、
| ||
C、
| ||
| D、3 |

 的值(
▲ )
的值(
▲ ) B.12 C.
B.12 C. D.32
D.32