题目内容
用一段长为10米的篱笆,一边靠墙围出一块苗圃.
(1)如图1,若围出的苗圃是△A1B1C1,A1C1=B1C1,靠墙部分A1B1=8米;如图2,若围出的苗圃是矩形A2B2C2D2,靠墙部分A2B2=5米.设△A1B1C1的面积为S1(m2),矩形A2B2C2D2的面积为S2(m2).试计算S1与S2的面积.
(2)如图3,若围出的苗圃是五边形A3B3C3D3E3,A3E3⊥A3B3,B3C3⊥A3B3,∠C3=∠E3=135°,∠D3=90°.若C3D3=D3E3=
| 2 |
(3)请你在图4中设计出一种围法,使围成的苗圃的面积大于(1)(2)中苗圃的面积.(说明你所围图形的特征,并计算它的面积)(比较大小时部分参考数据:
| 2 |
| 3 |
分析:(1)由于△A1B1C1是等腰三角形,所以A1C1=B1C1=5,过点C1作高,利用勾股定理求出高,即可求出面积.而对于矩形易求出长和宽分别是5和2.5.
(2)把五边形分割为矩形和三角形,再求解其面积.
(3)答案不唯一,可以是半圆.
(2)把五边形分割为矩形和三角形,再求解其面积.
(3)答案不唯一,可以是半圆.
解答: 解:(1)如图1,作C1M⊥A1B1与点M,
解:(1)如图1,作C1M⊥A1B1与点M,
由题意得,A1C1=B1C1=5,
又A1B1=8,
∴A1M=4,
根据勾股定理可得,MC1=
=3,
∴S1=
×8×3=12(m2),
在图2中,根据题意,易知A2B2=C2D2=5,
∴A2D2=B2C2=2.5,
∴S2=5×2.5=12.5(m2).
(2)连接E3C3,如图3,
∵∠D3=90°,C3D3=D3E3=
,
∴E3C3=2,
∴E3A3=5-
,
∴S3=
×
×
+2×(5-
)=11-2
(m2),
(3)不唯一,如围成半圆等.
设半圆的半径为r,
πr=10,∴r=
,
∴S半圆=
π(
)2=
.
 解:(1)如图1,作C1M⊥A1B1与点M,
解:(1)如图1,作C1M⊥A1B1与点M,由题意得,A1C1=B1C1=5,
又A1B1=8,
∴A1M=4,
根据勾股定理可得,MC1=
| 52-42 |
∴S1=
| 1 |
| 2 |
在图2中,根据题意,易知A2B2=C2D2=5,
∴A2D2=B2C2=2.5,
∴S2=5×2.5=12.5(m2).

(2)连接E3C3,如图3,
∵∠D3=90°,C3D3=D3E3=
| 2 |
∴E3C3=2,
∴E3A3=5-
| 2 |
∴S3=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(3)不唯一,如围成半圆等.

设半圆的半径为r,
πr=10,∴r=
| 10 |
| π |
∴S半圆=
| 1 |
| 2 |
| 10 |
| π |
| 50 |
| π |
点评:本题综合考查了勾股定理和圆知识的综合应用,难度不大.

练习册系列答案
相关题目
 园的面积y(米2)与x(米)的关系式为
园的面积y(米2)与x(米)的关系式为 用一段长为20米的篱笆围成一个一边靠墙的矩形菜园,墙长为12米,这个矩形的长宽各为多少时,菜园的面积最大,最大面积是多少?
用一段长为20米的篱笆围成一个一边靠墙的矩形菜园,墙长为12米,这个矩形的长宽各为多少时,菜园的面积最大,最大面积是多少?
 (m),五边形A3B3C3D3E3的面积为S3(m2),则它的面积应该为多少?
(m),五边形A3B3C3D3E3的面积为S3(m2),则它的面积应该为多少? ,
,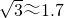 ,π≈3)
,π≈3)