题目内容
已知:关于x的方程x2-(m-1)x-2m2+m=0
(1)求证:无论m为何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且 x12+x22=2,求m的值.
(1)求证:无论m为何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且 x12+x22=2,求m的值.
考点:根的判别式,根与系数的关系
专题:
分析:(1)求出△的式子,再判断出其符号即可;
(2)先根据根与系数的关系得出x1+x2与x1•x2,的关系,代入x12+x22=2即可得出结论.
(2)先根据根与系数的关系得出x1+x2与x1•x2,的关系,代入x12+x22=2即可得出结论.
解答:解:(1)∵△=[-(m-1)]2-4(-2m2+m)
=9m2-6m+1
=(3m-1)2≥0,
∴方程总有实数根;
关于x的方程x2-(m-1)x-2m2+m=0
(2)∵此方程有两个实数根x1,x2,
∴x1+x2=m-1,x1•x2=-2m2+m,
∴x12+x22=(x1+x2)2-2x1•x2=(m-1)2-2(-2m2+m)=2,
解得m1=-
,m2=1.
=9m2-6m+1
=(3m-1)2≥0,
∴方程总有实数根;
关于x的方程x2-(m-1)x-2m2+m=0
(2)∵此方程有两个实数根x1,x2,
∴x1+x2=m-1,x1•x2=-2m2+m,
∴x12+x22=(x1+x2)2-2x1•x2=(m-1)2-2(-2m2+m)=2,
解得m1=-
| 1 |
| 5 |
点评:本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
若函数y=
,则当函数值y=8时,自变量x的值是( )
|
A、±
| ||
| B、4 | ||
C、±
| ||
D、-
|
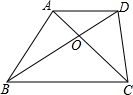 如图所示,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD:BC=2:3,求S△AOD:S△BOA.
如图所示,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD:BC=2:3,求S△AOD:S△BOA.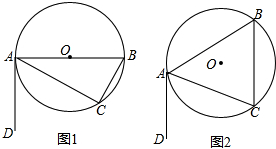 如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B.
如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B. 如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在
如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,再连接AA1,若∠1=20°,求∠B的度数?
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,再连接AA1,若∠1=20°,求∠B的度数?