Question

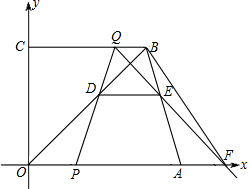在直角梯形OABC中，OA∥BC，A、B两点的坐标分别为A（10，0），（9，8），动点P、Q同时从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交x轴于点F（如图）．设动点P、Q运动时间为t（单位：秒），则当t=

 

时，△PQF是等腰三角形．

Answer 1

考点：直角梯形,坐标与图形性质,等腰三角形的判定

专题：动点型

分析：分三种情况进行讨论，让△PQF的三边两两相等，求出t的值．

解答：解：如图所示：过点Q作QH⊥x于点H，
①当QP=PF时，则

82+(9-t-2t)2

=10+2t-2t，
∴t₁=1，t₂=5（不合题意舍去）．
②当QP=QF时，则

82+(9-t-2t)2

=

82+FH2

，
即

82+(9-3t)2

=

64+FH2

=

82+[10+2t-(9-t)]2

，
解得：t=

4

3

．
③当QF=PF时，则

82+(1+3t)2

=10，
∴t=

5

3

或t=-

7

3

（不合题意舍去），
综上，当t=1或

4

3

或

5

3

时，△PQF是等腰三角形．
故答案为：t=1或

4

3

或

5

3

．

点评：本题综合考查了勾股定理的应用，等腰三角形的判定等的知识点；要注意的是分三种情况进行讨论，不可丢掉任何一种．