题目内容
2.(1)$\frac{2x}{{x}^{2}-9}$-$\frac{1}{x+3}$;(2)解方程:$\frac{x}{x-1}$+$\frac{1}{x}$=1.
分析 (1)原式通分并利用同分母分式的减法法则计算,约分即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{2x-(x-3)}{(x+3)(x-3)}$=$\frac{x+3}{(x+3)(x-3)}$=$\frac{1}{x-3}$;
(2)去分母得:x2+x-1=x2-x,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列哪个点一定在双曲线y=$\frac{6}{x}$的图象上( )
| A. | (1,5) | B. | (-1,6) | C. | (-1,-6) | D. | (2,-3) |
7.将分式$\frac{xy}{x+y}$中的x,y的值同时扩大10倍,则分式的值( )
| A. | 扩大100倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{10}$ |
8.一个物体向西移动5米记作-5米,这个物体又移动了若干米,停留在两次移动前的位置的西边1米处.能反映这个物体第二次移动的方向和路程的算式是( )
| A. | -1-(-5) | B. | 1+(-5) | C. | -1+(-5) | D. | 1-(-5) |
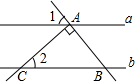 如图,直线a∥b,点A在直线a上,AB⊥AC垂足为A,若∠1=42°,则∠2为48度.
如图,直线a∥b,点A在直线a上,AB⊥AC垂足为A,若∠1=42°,则∠2为48度.