题目内容
7.点E与点F的纵坐标相同,横坐标不同,则直线EF与y轴的关系是( )| A. | 相交 | B. | 垂直 | C. | 平行 | D. | 以上都不正确 |
分析 由点E与点F的纵坐标相同,横坐标不同,可知直线EF与y轴的关系.
解答 解:∵点E与点F的纵坐标相同,横坐标不同,
∴直线EF与y轴垂直.
即直线EF与y轴的关系是垂直.
故选A错误,选项B正确,选项C错误,选项D错误.
故选B.
点评 本题考查坐标与图形的性质,解题的关键是明确与y轴垂直的直线上所有的点的纵坐标相等,横坐标不同.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
17.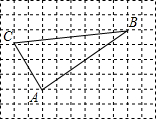 如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
 如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
2.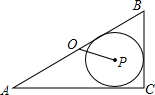 如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
 如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{5}$ | D. | $\frac{12}{5}$ |
12.已知二次函数y=ax2+bx+c的图象的顶点为(4,-2)且与x轴的两个交点为一正一负,则一次函数y=ax-2与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
19.下列各等式一定成立的是( )
| A. | a2=(-a)2 | B. | a3=(-a)3 | C. | -a2=|-a2| | D. | a3=-a3 |
16.下列说法正确的是( )
| A. | 32ab3的次数是6次 | B. | x+$\frac{1}{x}$不是多项式 | ||
| C. | x2+x-1的常数项为1 | D. | 多项式2x2+xy+3是四次三项式 |
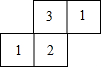 如图是若干个棱长为1cm的正方搭建成的几何体从上面看到的形状图,其中小正方形里的数字表示在该位置小正方体的个数.
如图是若干个棱长为1cm的正方搭建成的几何体从上面看到的形状图,其中小正方形里的数字表示在该位置小正方体的个数.