题目内容
2.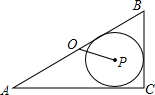 如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{5}$ | D. | $\frac{12}{5}$ |
分析 过点P作PD⊥AC,PE⊥BC,PF⊥AB,由点P是内切圆的圆心可知PD=PE=PF,再由切线长定理可知CD=CE,BE=BF,故可得出四边形PDCE是正方形,再由勾股定理求出AB的长,故可得出PD的长,由BE=BC-CE可得出BE的长,根据点O为直角三角形的外心可得出OB的长,进而得出OF的长,根据勾股定理即可得出结论.
解答  解:过点P作PD⊥AC,PE⊥BC,PF⊥AB,
解:过点P作PD⊥AC,PE⊥BC,PF⊥AB,
∵点P是内切圆的圆心,
∴PD=PE=PF,CD=CE,BE=BF
∴四边形PDCE是正方形.
∵△ABC中,∠C=90°,BC=6,AC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴PE=PF=PE=$\frac{6+8-10}{2}$=2,
∴BE=BF=6-2=4.
∵点O为△ABC的外心,
∴OB=$\frac{1}{2}$AB=5,
∴OF=OB-BF=5-4=1,
∴OP=$\sqrt{{OF}^{2}+{PF}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故选C.
点评 本题考查的是三角形的内切圆与内心,熟知直角三角形的内心与外心的求法是解答此题的关键.

练习册系列答案
相关题目
12.下列各式由左边到右边的变形,是因式分解的是( )
| A. | 3x(x+y)+3x2+3xy | B. | -2x2-2xy=-2x(x+y) | C. | (x+5)(x-5)=x2-25 | D. | x2+x+1=x(x+1)+1 |
7.点E与点F的纵坐标相同,横坐标不同,则直线EF与y轴的关系是( )
| A. | 相交 | B. | 垂直 | C. | 平行 | D. | 以上都不正确 |
12.下列函数中,是反比例函数的为( )
| A. | y=$\frac{1}{5x}$ | B. | y=$\frac{2}{{x}^{2}}$ | C. | y=2x+1 | D. | 2y=x |
 如图,是某校八(1)班学生在某一天各自课外阅读所有时间的条形统计图,根据图形回答下列问题:
如图,是某校八(1)班学生在某一天各自课外阅读所有时间的条形统计图,根据图形回答下列问题: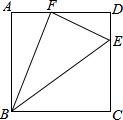 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若AB=4,AD=5,tan∠DFE=$\frac{3}{4}$,求sin∠FBE的值.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若AB=4,AD=5,tan∠DFE=$\frac{3}{4}$,求sin∠FBE的值.