题目内容
16.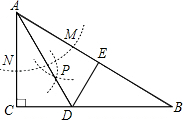 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以N、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP并延长BC于点D.过点D作DE⊥AB,垂足为E,连接CE.
如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以N、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP并延长BC于点D.过点D作DE⊥AB,垂足为E,连接CE.求证:(1)AD平分∠BAC;
(2)AD垂直平分CE.
分析 (1)连接NP,MP,根据SSS定理可得△ANP≌△AMP,故可得出结论;
(2)连接CE,易证△ACD≌△AED,由此可得AC=AE,又因为AD平分∠BAC,所以AD⊥CD,AD平分CE,即AD垂直平分CE.
解答 证明:(1)连接NP,MP,
在△ANP与△AMP中,
∵$\left\{\begin{array}{l}{AN=AM}\\{NP=NP}\\{AP=AP}\end{array}\right.$,
∴△ANP≌△AMP(SSS),
∴∠CAD=∠BAD,
∴AD平分∠BAC;
(2)连接CE,
在△ACD和△AED中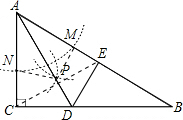
$\left\{\begin{array}{l}{∠CAD=∠EAD}\\{∠ACD=∠AED=90°}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED(AAS),
∴AD=AE,
又∵AD平分∠BAC,
∴AD⊥CD,AD平分CE,
即AD垂直平分CE.
点评 此题主要考查了基本作图,以及全等三角形的判定和性质以及等腰三角形的判定和性质,解题的关键是利用全等三角形的性质得到AC=AE,即△ACE是等腰三角形.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 在数轴上表示下列各数,并把它们按照从小到大的顺序排列:
在数轴上表示下列各数,并把它们按照从小到大的顺序排列: