题目内容
8．已知非零实数a、b、c，若2a2+4b2+c2=2a（2b-c），则$\frac{a+b-c}{a-b+c}$=-5．分析 首先把2a2+4b2+c2=2a（2b-c），变为（a-2b）2+（a+c）2=0，得出b=$\frac{1}{2}$a，c=-a，进一步代入代数式求得答案即可．
解答 解：∵2a2+4b2+c2=2a（2b-c），
∴a2-4ab+4b2+a2+2ac+c2=0，
∴（a-2b）2+（a+c）2=0，
∴a-2b=0，a+c=0．
∴b=$\frac{1}{2}$a，c=-a，
∴$\frac{a+b-c}{a-b+c}$=$\frac{\frac{5}{2}a}{-\frac{1}{2}a}$=-5．
故答案为：-5．
点评 此题考查因式分解的实际运用，非负数的性质，利用完全平方公式因式分解是解决问题的关键．
练习册系列答案
相关题目
已知数轴上的点A、B、C分别表示数a、b、c，用“＜”把数a、b、c、-a、-b、-c连接起来．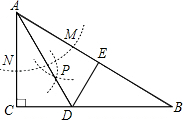
如图，在△ABC中，∠C=90°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以N、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，连接AP并延长BC于点D．过点D作DE⊥AB，垂足为E，连接CE．
有理数a，b在数轴上的位置如图所示，则（-a）+（-b）＜0（填“＞”或“＜”）
18．已知$\frac{a}{b}=\frac{b}{a}$，则a与b的关系一定为（ ）
| A． | a=b | B． | |a|=|b| | C． | a=|b| | D． | b=|a| |