题目内容
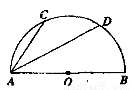
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:

(1)利用网格图确定该圆弧所在圆心D点的位置(保留画图痕迹),则写出D点坐标为 ;
(2)连结AD,CD,求⊙D的半径长为 (结果保留根号),∠ADC的度数为 ;
(3)求扇形DAC是一个圆锥的侧面展开图,求该圆锥的底面半径长.(结果保留根号)
(1)(-2,0)(2) ;90°;(3)
;90°;(3) .
.
【解析】
试题分析:(1)利用垂径定理得出D点位置即可;
(2)利用点的坐标结合勾股定理得出⊙D的半径长,再利用全等三角形的判定与性质得出∠ADC的度数;
(3)利用圆锥的底面圆的周长等于侧面展开图的扇形弧长即可得出答案.
试题解析:(1)如图所示:D点即为所求,坐标为:(-2,0);

(2)∵D(-2,0),A(0,4),
∴DO=2,AO=4,
∴AD= ,
,
即⊙D的半径长为 ,
,
∵C(-6,2),
∴EC=2,DE=4,
在△CDE和△DAO中,
 ,
,
∴△CDE≌△DAO(SSS),
∴∠CDE=∠DAO,∠ADO=∠ECD,
∴∠CDE+∠ADO=90°,
∴ADC=90°;
(3)设圆锥的底面圆的半径为r,根据题意得出:
 ,
,
解得:r= .
.
考点:圆的综合题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目


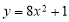 B.
B.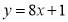 C.
C.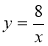 D.
D.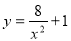

 B.3
B.3